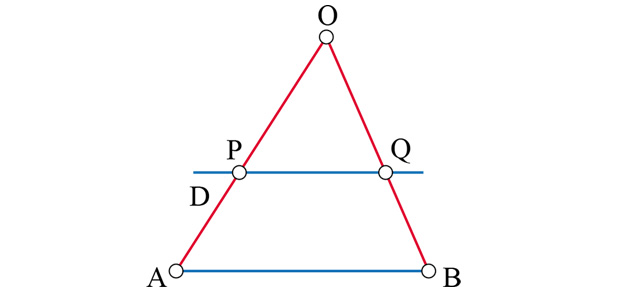
Dans sa version classique, le théorème de Thalès est un théorème de géométrie plane. Un triangle OAB et une droite D parallèle au côté [AB] sont donnés. La droite D coupe les deux côtés [OA] et [OB] en deux points, P et Q. 

Le théorème de Thalès fournit alors la relation numérique suivante :

La méthode la plus simple pour démontrer cette égalité fait intervenir les aires de certains triangles. Elle utilise un lemme concernant deux triangles OAB et OBC construits sur une même droite (ABC). Ils possèdent la même hauteur (OH).

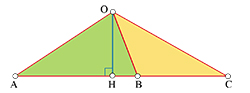
Leurs aires sont égales à la moitié des produits de OH par AB et BC, donc :

Ce résultat est valable dans toutes les configurations identiques, en particulier pour les triangles QOP et QPA d'une part et QOP et PQB d'autre part. On peut ainsi écrire :

Comme les deux triangles QPA et QPB ont la même base (PQ) et la même hauteur (la distance entre les deux droites (PQ) et (AB)), ils ont même surface. Les rapports d'aires sont donc égaux :  Le reste de la démonstration tient de l'algèbre.

Le théorème de Thalès reste vrai si on ne limite pas les côtés aux segments [OA] et [OB] mais qu'on les considère comme des droites ; P et Q peuvent alors être situés de l'autre côté de O, par exemple. Il convient dans ce cas de remplacer les longueurs par des mesures algébriques.

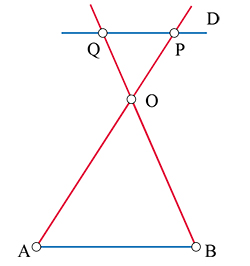Le théorème de Thalès fournit alors la relation suivante :

La démonstration ne demande que d'analyser les différents cas de figure. Il est également possible d'envisager la réciproque en considérant deux points P et Q des côtés [OA] et [OB] tels que

Peut-on en conclure que la droite (PQ) est parallèle au côté [AB] ? Pour examiner ce problème, introduisons la droite D passant par P et parallèle à (AB). Elle coupe le côté [OB] en un point Q'. D'après le théorème de Thalès :

L'hypothèse implique donc que  , donc Q = Q'. La droite (PQ) est bien parallèle à (AB).

En gardant les mêmes notations, le théorème de Thalès peut également s'écrire : si (PQ) est parallèle à (AB), alors 

Pour le démontrer, il suffit de remarquer que les triangles en jeu sont semblables.

Un point de vue plus moderne

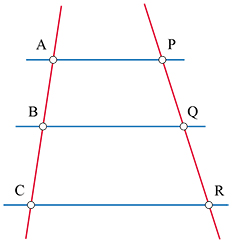On énonce également souvent le théorème de Thalès en considérant deux droites du plan (concourantes ou parallèles) et trois droites parallèles les coupant chacune en trois points (A, B, C et P, Q, R).

Le théorème de Thalès fournit alors la relation suivante :

La démonstration est évidente dans le cas où les droites (ABC) et (PQR) sont parallèles ; elle se ramène au cas classique, modulo un petit calcul algébrique, si elles sont concourantes. Cette troisième formulation se généralise à l'espace de dimension trois en remplaçant les trois droites parallèles par des plans parallèles. Les deux droites (ABC) et (PQR) n'ont pas besoin d'être coplanaires (c'est-à-dire dans un même plan).

Le théorème de Thalès fournit encore la relation

Il se généralise dans les dimensions quatre et supérieures. Il est nécessaire cependant de remplacer les plans parallèles en hyperplans parallèles.

Le théorème de Thalès est à l'origine de plusieurs applications théoriques, les plus directes concernent la géométrie du triangle. La plus importante est sans doute le théorème de Ménélaüs :

si ABC est un triangle et D une droite coupant ses trois côtés en P, Q et R, alors

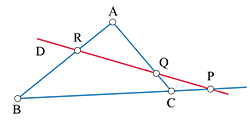Réciproquement, cette relation implique que les trois points P, Q et R sont alignés.

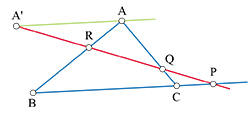
Le théorème de Thalès s'introduit grâce à la droite (AA') parallèle au côté [BC].

D'après le théorème de Thalès,

 et  ,

donc  

La réciproque vient de celle du théorème de Thalès. Le théorème de Ménélaüs peut également se montrer en reprenant l'idée de la démonstration du théorème de Thalès, c'est-à-dire en considérant les aires des triangles tels que PBR et PCR dont le rapport est celui de PB à PC. Le théorème de Ménélaüs est utile dans bon nombre de questions concernant les alignements de points.

Une autre application théorique du théorème de Thalès est le théorème de Ceva : si ABC est un triangle et P, Q, R trois points sur les côtés [BC], [CA] et [AB] respectivement, alors les droites (AP), (BQ) et (CR) sont concourantes ou parallèles si, et seulement si,

Ce théorème peut se démontrer soit à partir de l'un des théorèmes de Thalès et de Ménélaüs, soit directement à partir des aires. Il est utile dans les questions concernant des concourances de droites. En hommage à Ceva, les 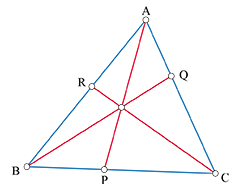droites d'un triangle passant par un sommet et coupant le côté opposé (telles que (AP), (BQ) et (CR)) sont dites des céviennes, les points sur le côté opposé (P, Q et R) sont appelés les pieds des céviennes, ce qui peut faire penser à une zone géographique française sujette aux inondations…