Si des phénomènes de régularité statistique avaient été observés et quantifiés dès le milieu du XVIII^e siècle par de grands mathématiciens comme de Moivre, Laplace et Gauss, il a fallu attendre le XX^e siècle pour que des formalisations complètes et des démonstrations convaincantes des propriétés soient proposées. On réduit souvent l'ensemble des lois des grands nombres au seul théorème dit « central limite ». Cette appellation est due au mathématicien George Pólya qui l'utilisa dans un article daté de 1920, qui s'intitulait « Über den zentralen Grenzwertsatz der Wahrscheinlichkeitsrechnung », ce que l'on peut traduire littéralement par « Sur le théorème central limite du calcul probabiliste ». Quel est le contenu de ce théorème ? Il concerne ce que l'on nomme la « convergence en loi », entendez par là « en loi de probabilité ». Ce résultat concerne des distributions de probabilité de variables et non ces variables en elle-même ! 

La distribution normale

La distribution normale possède l'agréable propriété de stabilité pour l'addition, qui fait que sa tabulation est aisée : toute combinaison linéaire de distributions normales indépendantes est également une distribution normale. Ce théorème possède une réciproque : si une somme de variables aléatoires indépendantes est normale, alors chaque terme de la somme l'est également ! Mais il y a beaucoup plus. Toute somme de variables indépendantes et équidistribuées (obéissant à la même distribution de probabilité, ce qui se note « i.i.d. » en référence à l'expression « indépendante et identiquement distribuées »), de variances finies, mais non nécessairement normales est asymptotiquement normale. 

Que recouvre ce vocabulaire ? Il reprend les résultats obtenus par le Français Paul Pierre Levy (1886 - 1971) et le Finlandais Jarl Waldemar Lindeberg (1876 - 1932) au début des années 1920. Curieusement, ces résultats n'ont pas bénéficié d'une grande diffusion : Alan Turing en redonna une démonstration dans sa thèse soutenue en 1935. Signalons que le mathématicien russe Alexandre Mikhaïlovitch Liapounov (1857-1918) a obtenu un résultat comparable sous d'autres hypothèses. Notons X_(n) la somme de n variables indépendantes et identiquement distribuées :

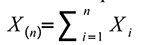
Les variables X_i sont supposées i.i.d. de moyenne μ et de variance finie σ². On en déduit que la variable somme X_(n) est de moyenne n.μ et de variance nσ². On peut réduire cette variable, ce qui consiste à mesurer ses écarts relatifs à sa moyenne en termes d'unités d'écart-type. Cette réduction de la variable est une étape indispensable au passage à la limite qui doit suivre.

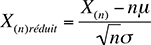
En effet, lorsque le nombre de termes de la somme croît et tend vers l'infini, sa moyenne (si elle n'est pas nulle) et sa variance divergent. En revanche, les variables réduites associées restent de moyenne nulle et d'écart-type unité. Le théorème central limite précise que la fonction de répartition de la variable X_(n) réduite converge, au sens de la convergence des fonctions, vers la fonction de répartition de la distribution normale de moyenne 0 et d'écart-type 1, lorsque le nombre de termes de la somme tend vers l'infini. En d'autres termes, pour un nombre n suffisamment grand, la valeur de la fonction de répartition de X_(n) réduite peut être approchée par la valeur de la fonction de répartition correspondante d'une distribution normale réduite, laquelle est tabulée et figure dans tous les manuels :

ce qui autorise tous les calculs de probabilité et s'avère donc d'une utilité essentielle.

Le théorème de Moivre-Laplace

Un cas particulier du théorème central limite est le théorème de Moivre-Laplace qui concerne la distribution binomiale. La variable « nombre de réussites » lors de la répétition de n expériences aléatoires indépendantes et identiques à deux issues est effectivement la somme de n variables i.i.d. du type « nombre de réussite lors d'une seule de ces expériences ». Ce cas particulier est intéressant : il montre clairement le type de convergence qui est concerné. En effet, la distribution normale est continue, à valeurs dans les réels. La distribution binomiale est discrète et à valeurs dans les naturels. Il est donc clair que la variable binomiale ne peut devenir une variable normale. Par contre, tous les calculs de probabilité associés à une variable binomiale peuvent être approchés au moyen d'une table de valeurs d'une normale réduite.

Le théorème central limite est particulièrement utile en statistique inférentielle, c'est-à-dire celle qui cherche à induire des résultats sur une population en partant d'échantillons. En effet, moyenne et variance d'un échantillon constituent de fait des sommes de variables aléatoires identiquement distribuées. Si l'échantillon prélevé est aléatoire simple, c'est-à-dire que l'on a attribué à chaque individu de la population considérée une probabilité identique d'être tiré au sort, les observations sont aussi indépendantes. On en déduit que la distribution de probabilité de ces moyennes et variances doit s'approcher d'une distribution normale. La grande majorité des tests statistiques reposent sur ces considérations.

Du théorème central limite aux lois des grands nombres

D'autres résultats s'intéressent à la convergence des variables en elle-même. On distingue des lois dites « faibles » et d'autres « fortes » des grands nombres. Les lois faibles concernent la convergence en probabilité. Considérons une suite de variables (X_n). Cette suite de variables converge en probabilité vers une variable X lorsque pour tout ε strictement positif, la probabilité associée à l'ensemble des événements pour lesquels X_n et X diffèrent de plus qu'ε, tend uniformément vers 0 lorsque n croît :

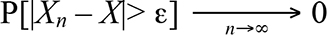
On remarque que ce résultat prenant en compte les variables est plus contraignant que celui découlant du théorème central limite. Deux variables ayant même distribution de probabilité et donc même fonction de répartition, peuvent être très différentes. Considérons un jeu équilibré de type « pile ou face » entre deux joueurs en décidant d'un gain g en cas de victoire d'un des joueurs et donc d'une perte identique en valeur absolue pour l'adversaire. La fonction de répartition de la variable « gain » des deux joueurs est identique. Mais quel que soit le résultat d'une partie, la différence entre les variables aléatoires « gain du joueur 1 » et « gain du joueur 2 » sera toujours égale à 2g.

Il y a plusieurs lois faibles. L'une des plus connues est attribuée au mathématicien Pafnouti Lvovitch Tchebychev (1821-1894) en référence à l'inégalité qui porte son nom et qui intervient dans la démonstration de la loi faible. Sous certaines conditions, elle exprime que la somme pondérée uniformément d'une suite de variables converge en probabilité vers la somme pondérée de leurs moyennes théoriques.

D'autres résultats comparables mais reposant sur des hypothèses alternatives ont été proposées par le mathématicien Russe Alexandre Khintchine (1878-1959). Les lois fortes des grands nombres prennent en compte un concept plus fort encore que celui de convergence en probabilité, à savoir la convergence presque sûre. Une suite de variables (X_n) converge presque sûrement vers une variable X si la probabilité associée aux événements pour lesquels la convergence des variables a lieu est égale à 1. L'ensemble pour lequel cette convergence des variables n'a pas lieu est donc de probabilité nulle : c'est un événement stochastiquement impossible.

Deux lois fortes furent démontrées dès 1929 par le père de l'axiomatique du calcul des probabilités, le mathématicien russe Andreï Kolmogorov (1903-1987). Elles concernent toutes deux la convergence presque sûre sous certaines conditions, des sommes pondérées uniformément de variables aléatoires. Ce résultat valide donc les estimations de nos moyennes usuelles. Il prouve que cette mesure de tendance centrale peut être approchée avec pertinence et « presque certitude » . Nous voilà rassurés : les moyennes arithmétiques nous renseignent correctement sur la tendance théorique des phénomènes mesurés ! Reste encore à déterminer si la moyenne, en tant que mesure de tendance centrale, est pertinente, ce qui est un autre problème.