En sciences, le hasard serait un aveu de faiblesse, un paradoxe, un domaine honteux ! Un aveu de faiblesse car, chaque effet ayant une cause, invoquer le hasard de l'occurrence d'un effet, c'est ne pas avoir établi un bon diagnostic de sa cause. Un paradoxe, car le hasard a ses lois, la plus célèbre étant la loi normale. Et ce serait enfin un domaine honteux car dédaigné des mathématiciens purs de la veine bourbakiste. Pourtant, le physiologiste britannique Francis Galton (1822–1911) écrivit son admiration de l'ordre qui naît du hasard : « Je ne connais presque rien d'aussi impressionnant que la merveilleuse forme de l'ordre cosmique exprimée par la Loi de fréquence des erreurs… Elle règne sereinement et avec retenue au milieu de la plus folle confusion. » 

Par « Loi de fréquence des erreurs », on aura reconnu la loi normale. Depuis, la physique quantique a introduit un hasard nécessaire… et fondamental : Dieu joue aux dés. La loi normale a longtemps été dénommée loi de Laplace en France et loi de Gauss dans les pays anglo-saxons. Tentons un consensus en la dénommant loi de Laplace-Gauss, bien que les approches des deux mathématiciens soient différentes…

Gauss : la voie astronomique

Gauss imagina la loi normale pour améliorer les observations astronomiques de son ami et collègue Heinrich Olbers. Le mathématicien allemand n'observait lui-même que très occasionnellement les objets célestes, mais il s'intéressait à la position des objets lumineux pour distinguer les planètes ou les astéroïdes mobiles des étoiles fixes (compte tenu de la rotation de la Terre) et pour calculer leurs trajectoires. Gauss avait donc calculé la trajectoire de Cérès, le premier astéroïde découvert (entre Mars et Jupiter), sur la base des observations de Olbers, lequel détecta ensuite la présence d'un objet mobile dans la région où Cérès était censé se trouver selon les calculs de Gauss. C'était l'astéroïde Pallas, qui passait fortuitement près de Cérès. Comment connaître au mieux la position A d'un corps céleste à la suite de diverses mesures A₁, A₂… A_n ? La différence A_i – A entre la mesure numéro i et la position réelle correspond à la valeur de l'erreur commise sur la position du corps céleste. Pour calculer A, Gauss a inventé la célèbre méthode des moindres carrés, qui consiste à calculer la valeur de A minimisant la somme des carrés des différentes valeurs A_i – A. Il a montré que cette valeur correspondait à la moyenne A_moy des n observations A₁, A₂… A_n. Gauss s'intéresse également à la répartition des erreurs autour de la moyenne, et pour cela propose une autre méthode de calcul. Il suppose que les erreurs sont indépendantes et dénomme P(x_i) la probabilité de commettre l'erreur x_i = A_i – A lors de l'observation A_i. Pour cela, il introduit la fonction de vraisemblance V(A), égale au produit des probabilités P(x_i), qui est la probabilité que cette série d'erreurs ait été commise lors des mesures. Il émet deux hypothèses : la fonction P est symétrique par rapport à la valeur A_moy (la probabilité de mesurer une certaine valeur inférieure à A_moy est égale à la probabilité de mesurer la même valeur supérieure) et diminue quand la valeur absolue de l'erreur A_i – A_moy augmente. Gauss démontre que les fonctions qui satisfont ces deux conditions sont les fonctions du type . L'estimation de la position A par la méthode des moindres carrés coïncide avec son estimation par la méthode du maximum de vraisemblance ! De plus, la loi normale est la seule loi assurant cette propriété.

La vision de Laplace

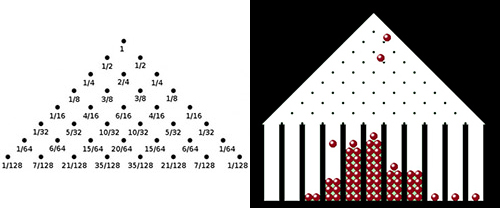
Les nombres de billes dans les godets situés en bas de la planche de Galton sont répartis selon une loi binomiale. À droite, les probabilités de rebond sur chaque plot. Lorsque le nombre de billes augmente, la loi de répartition binomiale approche la loi normale.

Laplace a une vision toute différente, fondée sur une extension de la loi binomiale d'Abraham de Moivre (1667–1754). Prenons la suite de billes sur une planche de Galton, qui illustre la tendance de la loi binomiale vers la loi normale. Chaque bille tombant par la gravité du haut de la planche verticale est déviée, par les plots, soit vers la gauche, soit vers la droite, avec une probabilité égale à 1 / 2. La trajectoire moyenne des billes est verticale, et elles remplissent les godets situés au voisinage de l'axe de symétrie de la planche. Quelques billes s'éloignent du trajet moyen et sont recueillies par des godets loin de l'axe. Désignons par x le nombre de rebonds vers la gauche sur les N lignes de plots. La probabilité de cette valeur de x est C(N, x) / 2^N, où C(N, x) est le nombre de combinaisons de x objets pris parmi N. La quantité C(N, x) est explicitement égale à N! / (x! (N – x)!), où N! désigne le produit des entiers de 1 à N. Le nombre de billes dans chaque godet est régi par la loi dite binomiale, ainsi nommée car C(N, x) est le coefficient de ax dans le développement du binôme (1 + a)^N, pour 0 ≤ x ≤ N. Lorsque la valeur de N augmente, la répartition des billes s'approche de la courbe en cloche représentative de la loi normale (cette évolution avait été démontrée par de Moivre en 1733). Laplace va plus loin et rejoint Gauss dans l'analyse des erreurs d'observation. En désignant par x_i l'erreur effectuée sur la i-ème mesure, il s'intéresse à la somme S_n = x₁ + x₂ + … + x_n, les x_i étant des variables aléatoires indépendantes. À quelles conditions la somme S_n est-elle approchée par la loi normale pour de grandes valeurs de N ? Laplace démontre qu'une des conditions essentielles est réalisée quand les erreurs x_i sont indépendantes et obéissent à la même loi. Tel est le cas dans l'expérience de la planche de Galton.  

À gauche, une marche au hasard sur une droite. Chaque déplacement vers la droite ou la gauche est tiré au hasard avec une probabilité égale à 1 / 2. À droite, la simulation d'un mouvement brownien par une marche au hasard : à chaque tirage, le point représentatif va vers le haut en se déplaçant d'une unité avec la probabilité 1 / 2 d'aller ensuite soit vers le haut avec une pente de 45°, soit vers le bas avec une pente de –45°.

La marche au hasard illustre la répartition envisagée par Laplace autour de la moyenne. En partant de l'origine O, on tire à pile ou face le déplacement d'un point d'une unité vers la gauche pour pile et d'une unité vers la droite pour face. Après N tirages, le point coïncidera en moyenne avec l'origine, mais pour de grandes valeurs de N, le déplacement du point se répartit autour de la valeur moyenne 0 selon une loi normale d'écart type  , c'est-à-dire que dans 66,8 % des cas, le déplacement sera dans un intervalle plus ou moins   autour de zéro. La loi normale de Laplace-Gauss aura de multiples ramifications à mesure du développement des mathématiques et des diverses sciences. Carl Friedrich Gauss et Pierre-Simon Laplace avaient-ils pressenti la portée immense de leurs lois ? Nul ne peut le dire. Toutefois, pourquoi ne pas identifier les mathématiciens de génie au poète célébré par Victor Hugo ? Selon l'homme de lettres, en effet :

« Des temps futurs perçant les ombres,
Lui seul distingue en leurs flancs sombres
Le germe qui n'est pas éclos. »