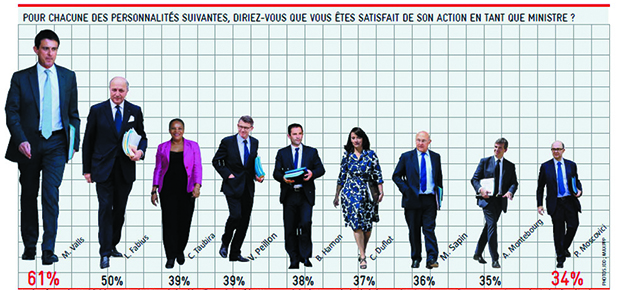
Depuis une quarantaine d'années, avant chaque élection, un grand nombre de sondages, parfois contradictoires, nous livrent ce que serait le résultat du vote si nous votions le jour même. D'autres sondages sont effectués, à visée commerciale en particulier. Mais quelle est leur fiabilité ?
Un peu d'histoire
On attribue à George Gallup la paternité des sondages d'opinion. Cet Américain, originaire de l'Iowa, propose de prédire le vainqueur de l'élection présidentielle américaine de 1936. En partant d'un échantillon de 50 000 personnes, il pronostique la victoire du président sortant Franklin Roosevelt avec 56 % des voix, contredisant l'avis du Literary Digest qui, sur la foi d'un questionnaire ayant reçu deux millions quatre cent mille réponses, annonçait la victoire du républicain Landon. Le succès écrasant du candidat démocrate avec 61 % des suffrages, montra pour la première fois qu'un échantillon bien choisi était plus efficace qu'un autre, quarante fois plus important, mais comportant un biais évident, celui des non-réponses en l'occurrence.
Le sociologue français Jean Stoetzel rencontre Gallup en 1937 et voit l'intérêt de ce type d'enquêtes pour mieux comprendre le comportement des individus. Il fonde à son retour l'Institut français d'opinion publique (IFOP) et sonde aussitôt les Français avec la question Approuvez-vous les accords de Munich ? Seulement 57% des sondés répondent par l'affirmative, alors que cette question obtient une majorité de 87 % à la Chambre de Députés. L'IFOP acquerra lors de l'élection présidentielle de 1965 une grande notoriété en prédisant le ballotage du Général de Gaulle face à François Mitterrand.
La théorie mathématique proprement dite sous-jacente aux sondages est en réalité simple. On souhaite connaître l'opinion d'une population N très importante, par exemple l'ensemble des citoyens français, à une question possédant deux (ou plusieurs) réponses. Il est évidemment hors de question d'interroger de manière exhaustive tout le monde. La méthode consiste à sélectionner un échantillon « au hasard » parmi cette population et de considérer que le taux de réponses positives des individus choisis est suffisamment proche de la réalité. Il importe aussi d'évaluer un majorant de l'erreur commise.
Plus précisément, supposons que le pourcentage de réponses positives à cette question soit p avec un écart type . Considérons alors l'ensemble des échantillons théoriques de taille n extraits de la population initiale. Le théorème central limite nous informe que si n est grand, la population des échantillons suit approximativement une loi normale de même moyenne p et de variance (carré de l'écart type)
. On peut alors encadrer, avec un risque d'erreur relativement faible, le taux de réponse positive sur la population totale dans un intervalle de confiance (voir encadré). Il va de soi que plus on souhaite minimiser l'erreur, plus l'intervalle de confiance va être grand et donc le résultat imprécis. Selon le contexte, on peut accepter une plus ou moins grande précision. Qu'une marque de pâtes veuille savoir quel pourcentage de la population préfère le riz aux pâtes ne nécessite pas une même précision que prévoir le résultat d‘une élection présidentielle indécise. Dans ce dernier cas, pour y parvenir, les instituts spécialisés utilisent des recoupements plus fins qu'ils gardent généralement secrets.
