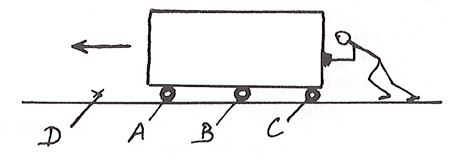
Quand on veut déplacer un objet lourd et volumineux, par exemple un coffre, sur un sol à peu près horizontal, on ménage beaucoup sa peine en plaçant des « rouleaux » entre le sol et l’objet. Comme on le voit sur le schéma, plusieurs rouleaux A, B, C… sont nécessaires. Quand le coffre avance dans la direction de la flèche, le rouleau C échappe vers l’arrière : il faut que quelqu’un vienne le prendre, et aille le placer en avant du coffre (vers D).

Des rouleaux qui ne roulent pas

Les rouleaux limitent les efforts pour déplacer le coffre mais ont un inconvénient : ils roulent très facilement si le sol est en pente… Comment pourrait-on avoir des rouleaux permettant de déplacer un coffre avec le minimum d’efforts, et qui ne rouleraient pas d’eux-mêmes sur un sol en pente ? La figure suivante vous propose un « rouleau à section triangulaire » qui ne roule sûrement pas tout seul. L’ennui, c’est que si l’on pose un coffre sur la pointe C et qu’on le pousse, soit il doit glisser sur la pointe C (et c’est alors aussi dur que si le coffre était posé à même le sol), soit le « rouleau » bascule en pivotant autour de B. Mais c’est très difficile puisque le coffre doit « monter » de C en C’.

En fait, cela ne « roule » pas ! Le triangle équilatéral ne peut donc pas servir comme rouleau. Mais rien ne nous empêche de chercher à le perfectionner.

La figure suivante montre la coupe d’un rouleau où le triangle équilatéral ABC est complété par des arcs de cercles ayant tous le même rayon (égal à AB). Si le coffre à déplacer repose sur la « pointe » C, quand on pousse le coffre vers la gauche, le rouleau triangulaire pivote sans effort puisque sa base arrondie entre A et B joue le rôle d’une véritable roue.

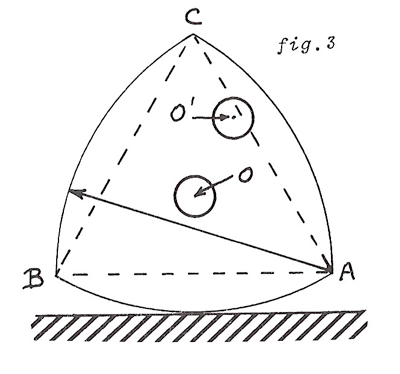
Encore mieux : le point C qui supporte le coffre va se déplacer vers la gauche sans changer de hauteur ! Il en découle un minimum d’efforts pour déplacer le coffre. Enfin, un rouleau dont la section ressemble à la figure ne roule pas tout seul. Il a été décrit par le mécanicien allemand Franz Reuleaux et porte désormais son nom, triangle de Reuleaux, ou orbiforme équilatérale (voir le dossier « Constructions mécaniques de courbes », Tangente 151, 2013).

Cet objet étonnant est formé de trois arcs de cercles centrés aux sommets d’un triangle équilatéral (courbe continue, mais avec trois points anguleux, au contraire des exemples précédents). On peut généraliser cette construction à un polygone régulier quelconque.

 
Des trous excentrés

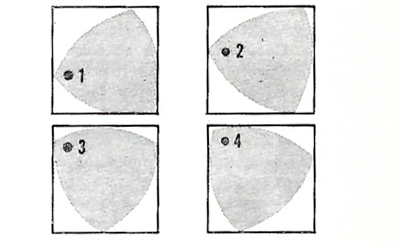
En associant par paires ces triangles curvilignes à l’aide d’un axe, tels des roues et leurs essieux, on constatera avec surprise que les pièces jouent leur rôle, quel que soit le positionnement des essieux dans les trous O ou O’.

Comme chaque roue possède deux trous, il y a trois positionnements possibles de l’axe :

• dans le trou central de chaque roue (de centre O) ;

• dans le trou excentré de chaque roue (de centre O’) ;

• dans un trou central et un trou excentré.

Dans tous les cas, chaque roue conserve une « largeur » constante qui permet à la plaque de la figure de se déplacer, sans secousse et parallèlement au sol, toujours à la même hauteur (voir Courbe auto-parallèle, courbe de largeur constante sur le site Mathcurve de Robert Ferréol, www.mathcurve.com).

Les triangles de Reuleaux font partie des courbes à largeur constante, tout comme le cercle (voir FOCUS), et leur étude est passionnante pour les mécaniciens et les physiciens. Ils sont employés dans de nombreux montages : appareils de projection cinématographique, mèche à faire des trous carrés (dans ce cas, en fait, le foret, ou plutôt la fraise, n’est pas lui-même carré, c’est sa forme et son axe décalé qui, lorsqu’il est mis en rotation, créent un trou carré).

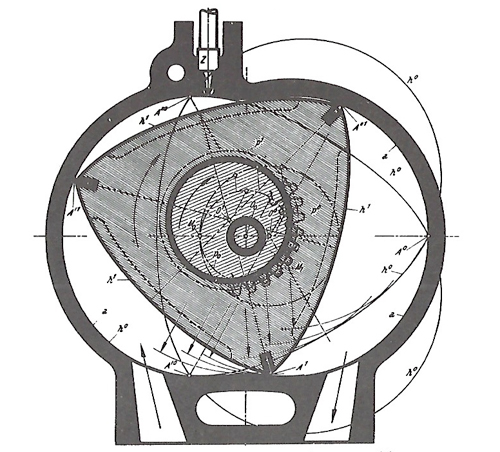
Coupe du moteur rotatif de Wankel.

Ce type de mèche fut décrit en 1914 par un ingénieur britannique, vivant en Pennsylvanie (États-Unis), James Harry Watts, puis breveté et commercialisé à partir de 1917.

Il faut surtout évoquer le fameux moteur rotatif dû à l’ingénieur allemand Felix Heinrich Wankel (1902–1988). Le fonctionnement en est relativement simple, avec un « piston » triangulaire (le stator), au centre d’une chambre (le rotor), permettant de délimiter trois chambres de combustion. Chacune de ces chambres effectue le cycle standard à quatre temps (admission, compression, explosion, échappement) en un tour de 360°. Pas de soupape ni d’arbre à cames : peu de pièces sont en mouvement, ce qui laisse présager la possibilité de régimes très élevés ! Les autres avantages de cette forme sont un poids moindre, un faible encombrement, une large plage d’utilisation et un rapport puissance/cylindrée très élevé.

Pourtant, un à un, presque tous les constructeurs abandonnent le moteur Wankel par suite d’une consommation importante, comparée aux moteurs traditionnels à essence, et à des coûts de développement élevés, en particulier pour garantir la fiabilité. À la fin des années 1970, le seul constructeur à croire encore au rotatif est Mazda, dont le savoir faire en la matière va petit à petit devenir unique.

La victoire du constructeur automobile japonais aux vingt-quatre heures du Mans, en 1991, avec un véhicule équipé de quatre rotors de 650 cm³ chacun et délivrant 700 ch, récompense sa persévérance et l’intérêt du moteur rotatif. Elle ne règle cependant pas le coût au kilomètre, lié au prix du carburant.

Des pièces de monnaie économes !

Il est possible de généraliser le triangle de Reuleaux à la plupart des polygones convexes (hexagone, heptagone…) et même dans l’espace (où l’on peut construire des tétraèdres de Reuleaux). C’est ainsi que les pièces britanniques de vingt et cinquante pence ont la forme d’un heptagone de Reuleaux, ce qui permet d’économiser du métal par rapport au cercle sans gêner la reconnaissance de ces pièces par les automates rendant la monnaie (les automates mesurent en effet une largeur identique, quelle que soit l’orientation des pièces).

Une pièce de vingt pence.

Le Chinois Guan Baihua a, de son côté, patiemment réalisé une curieuse bicyclette à « roues de Reuleaux » : les roues sont pentagonale à l’avant, triangulaire à l’arrière (voir Tangente 173, 2016).

Enfin, aucun de nos lecteurs ne s’étonnera que le regretté Martin Gardner ait traité, dans l’une de ses chroniques, des courbes à largeur constante, avec le luxe de détails et de références bibliographiques qui lui est coutumier. Nul doute cependant que de nombreuses et merveilleuses applications de ces « courbes de Reuleaux » restent à découvrir.