Alexandre Grothendieck (1928–2014) a laissé derrière lui environ cent mille pages de notes et textes divers, dont au moins seize mille portant sur des sujets mathématiques (voir Tangente 189, 2019). Que leur publication sur Internet soit ici l’occasion de revenir sur leur contenu aussi bien que sur la vie, la carrière et l’immense aura scientifique de leur auteur.

Alexandre Grothendieck en 1951, photographié par Paulo Ribenboim après avoir parcouru à vélo les quelque trente kilomètres qui séparent Nancy de Pont-à-Mousson (Meurthe-et-Moselle).

 L’homme de tous les refus

La vie du mathématicien Alexandre Grothendieck n’a certes pas été « un long fleuve tranquille » (voir notre dossier dans Tangente 162, 2014). Il est né en 1928 à Berlin d’un père anarchiste russe, qui mourra en déportation, et d’une mère journaliste allemande, dont il partagera un temps la vie en camp d’internement en France avant d’en être séparé pour effectuer sa scolarité, et qu’il ne retrouvera qu’en 1945. Après des études de mathématiques à Montpellier (Hérault), une thèse en 1950, Produits tensoriels topologiques et Espaces nucléaires, un passage au groupe Bourbaki, un poste universitaire à Sao Paulo (Brésil) et à Chicago (États-Unis) entre 1953 et 1958, il s’établit à l’Institut des hautes études scientifiques (IHES), qui s’installera très vite à Bures-sur-Yvette dans l’Essonne (1958–1970). Là, son séminaire de géométrie algébrique crée l’évènement et contribue largement à la réputation du lieu.

Grothendieck avait entre-temps déjà manifesté une première opposition, au service militaire pour obtenir la nationalité française. S’ensuit le départ pour l’étranger de 1953, et son long statut d’apatride.

D’autres refus, nombreux, ont suivi, jalonnant sa vie de personnage rebelle. Il obtient la médaille Fields en 1966, mais refuse de se rendre à Moscou pour la recevoir (pour cause de répression du soulèvement hongrois en 1956 et suite au traitement des écrivains Yuri Daniel et Andreï Siniavski par le pouvoir soviétique).

Il démissionne en 1970 de l’IHES, en partie semble-t-il par protestation contre le financement partiel de l’institut par le ministère de la Défense.

Naturalisé français en 1971, professeur au Collège de France puis à l’université de Montpellier, il décline le prestigieux et richement doté prix Crafoord (dont il dit n’avoir pas besoin pour vivre), qu’il devait partager avec son ancien élève Pierre Deligne en 1988.

Il refuse encore un livre hommage, The Grothendieck Festschrift (Springer, 1990, trois volumes), collection d’articles en son honneur à l’occasion de son soixantième anniversaire, rédigés sous la direction de Pierre Cartier.

À partir de 1990, il se retire à Lasserre, dans l’Ariège, rejetant cette fois tout contact avec ses anciennes relations. En rupture définitive avec le monde, il ne daignera même pas recevoir, en juillet 2014, le mathématicien américain John Tate, venu exprès, à 89 ans, pour le rencontrer une dernière fois. Que de refus dans cette vie par ailleurs si glorieuse en mathématiques !

Lasserre, ce petit village de l’Ariège où l’on ne vient pas par hasard.

Vocabulaire d’enfant, idées de génie

Chez Alexandre Grothendieck (« Shourik », pour ses proches), les liens entre objets mathématiques priment sur les objets eux-mêmes, ce point de vue induisant un changement fondamental de conception, les mathématiques tournant jusqu’alors autour des notions d’ensembles et d’objets. Il va donc forger des concepts et un vocabulaire traduisant ces nouvelles connexions. Il choisira pour cela des termes simples, compréhensibles par tous, même s’ils recouvrent une réalité mathématique beaucoup plus élaborée. Les notions phares qu’il introduit sont celles de schémas, de topos, de motifs, et celle de dessins d’enfant.

Avec les schémas, Shourik invente une classe de structures géométriques généralisant les variétés (une courbe, par exemple, est une variété de dimension 1, une surface une variété de dimension 2). Le terme « schéma », inventé par Claude Chevalley mais « popularisé » par Grothendieck, permet d’identifier un anneau commutatif (c’est-à-dire un ensemble d’objets sur lesquels on a défini une addition qui en fait un groupe commutatif, et une multiplication elle aussi commutative, associative et distributive sur l’addition) à son spectre, c’est-à-dire l’ensemble de ses idéaux premiers (sous-groupes additifs stables par multiplication d’un élément de l’anneau, tels que, en plus, pour tout produit ab appartenant à l’idéal, ou a ou b lui appartiennent également). C’est en quelque sorte cet « éventail magique » dont parle le mathématicien qui « fournit un efficace principe de passage pour relier entre elles des variétés ressortissant de géométries qui jusque-là étaient apparues comme plus ou moins isolées ». Il appelle cela la géométrie schématique et la considère comme une première ébauche de la géométrie arithmétique dont il rêve.

Autre concept emblématique des mathématiques de Grothendieck : les topos, qui constituent une généralisation de la topologie classique des ensembles de points. À chaque espace topologique est associé un topos, et c’est cette correspondance, faisant passer des espaces ordinaires aux topos, que Shourik appelle la « traversée du miroir ». Pour lui, du côté des topos, « le monde est plus beau ». 

Rêve ultime de Grothendieck, les motifs apparaissent dans son vocabulaire à partir de 1964. Toujours dans un souci d’homogénéisation de théories disjointes, le mathématicien a remarqué que, même différentes les unes des autres, les façons de mesurer des quantités invariantes (comme le nombre de trous d’une surface par exemple) se « ressemblent » bien souvent beaucoup. Tout se passe, dit-il, comme si l’on était en présence de « développements thématiques différents », chacun dans le « tempo », dans la « clef » et dans le « mode » (majeur ou mineur) qui lui est propre, d’un même « motif de base ». C’est cette structure mathématique commune qui constitue le motif.

Dans ses textes, en particulier dans son ouvrage Récoltes et Semailles, Alexandre Grothendieck fait souvent référence à des arguments « d’une simplicité enfantine », se demandant pourquoi il n’y avait pas pensé plus tôt. C’est donc tout naturellement qu’il va, dans son Esquisse d’un programme, introduire la notion de dessins d’enfant. Ce sont pour lui des graphes tracés sur des surfaces compactes (comme par exemple la sphère ou le tore) possédant quelques propriétés particulières et qui vont permettre d’énumérer certaines classes d’isomorphismes. Les sommets de ces graphes sont de deux couleurs, les extrémités d’une même arête ayant des couleurs différentes.

Un dessin d’enfant.

Schémas, topos, motifs, dessins d’enfant, on retrouve évidemment tous ces termes et leurs développements dans les archives du génial mathématicien, ouvertes en mai 2017 au public. Même s’ils sont présents aujourd’hui dans bien des travaux de géométrie algébrique ou de théorie des nombres, Grothendieck n’aura de son vivant pas eu le temps de leur donner l’amplitude qu’il souhaitait.

Des archives chargées de mystère

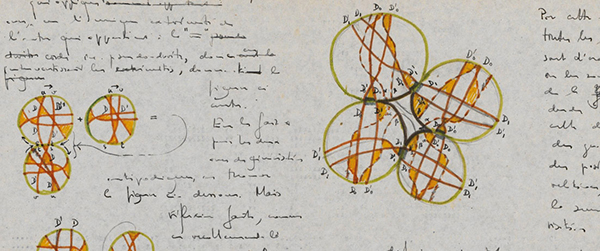
L’une des pages d’archives sur les pseudo-droites,
extraite de la partie traitant d’« espaces stratifiés ».

Ayant vécu en ermite à Lasserre en Ariège entre 1991 et 2014, ce génie de la géométrie algébrique a laissé derrière lui des milliers de pages écrites ou tapées à la machine. Seize mille pages sur les vingt-huit mille que cet éminent mathématicien a accumulées au cours de sa carrière professionnelle, entre 1949 et 1991 et laissées à l’Institut montpelliérain Alexandre-Grothendieck, ont été numérisées par l’université de Montpellier. La partie « ariégeoise », comptant environ soixante-dix mille pages, est entreposée dans une cave parisienne, avant (espère-t-on) d’être confiée à la Bibliothèque nationale de France.

Le fonds montpelliérain, légué par son auteur à son ancien élève Jean Malgoire, est constitué de documents qui ne sont classés ni de manière thématique, ni de manière chronologique. Heureusement, il a été possible de reconstituer leur organisation. On y trouve ainsi les réflexions de Grothendieck sur son procès de 1978 (pour avoir hébergé un moine bouddhiste japonais dont le titre de séjour avait expiré).

Les mathématiciens Georges Maltsiniotis (université Paris-VII) et Matthias Künzer (université de Stuttgart) ont par exemple rendu lisibles et publié certains des derniers écrits de la période « publique » d’Alexandre Grothendieck, entre 1990 et 1991, concernant les « dérivateurs ». En 2010, cependant, Grothendieck interdit toute publication ou réédition de son œuvre. Il a fallu attendre son décès en 2014 et la découverte d’un testament pour que l’interdiction soit levée.

Restent maintenant les textes de la période ariégeoise de « Shourik », qui renferment encore sûrement bien des secrets. Les premières investigations ont permis d’y découvrir des textes de géométrie algébrique assez classiques et élémentaires, ou des réflexions philosophiques comme Structure de la psyché. Ces milliers de pages, sont-elles donc d’une « richesse accablante » comme disait leur auteur, ou alors « de simple gribouillis », comme il qualifiait parfois ses écrits ?