
Le 1er juin 2019, Michel Serres s’est éteint (voir Tangente 189). Il se définissait lui-même comme un « scientifique devenu philosophe ». Il a en fait commencé par entreprendre des études de mathématiques, est passé ensuite par l’École Navale, pour bifurquer – sans doute sous l’influence d’un questionnement personnel sur la science, qui avait failli lors du drame d’Hiroshima – vers l’École normale supérieure (ENS), section « lettres », avant de devenir le philosophe et historien des sciences bien connu, qui a ravi son public par ses interventions médiatiques et ses multiples ouvrages. Il a gardé de ses premiers penchants pour les mathématiques une proximité avec cette discipline, au point de parsemer très fréquemment son parcours philosophique de jalons mathématiques qu’on retrouve aussi bien dans ses prises de parole que dans ses publications.
Leibniz, le point de départ
C’est le philosophe et mathématicien allemand Gottfried Wilhelm Leibniz (1646–1716) que Michel Serres a choisi comme sujet de sa thèse de philosophie, qui sera publiée aux Presses universitaires de France en 1968 car, dit-il, « Leibniz est de notre temps, il est notre prédécesseur, il a commencé de construire le monde où nous vivons, il l’a reconnu avant nous, mieux que nous ».
Sous le titre le Système de Leibniz et ses modèles mathématiques, il passe au crible l’œuvre de son illustre aîné et y découvre, même si le philosophe allemand a la réputation de se disperser, un système parfaitement cohérent, qu’il met en évidence à sa façon. « L’épaisseur du langage métaphysique empêche que cette lecture [d’une langue universelle] soit aussi aisée qu’on croit […]. Pour clarifier le problème, un principe s’impose : remonter des paradigmes [les modèles] à la structure […]. On pouvait alors choisir les modèles en mille domaines […]. On a préféré opérer une réduction vers le simple et choisir une succession de théories mathématiques. » En trois parties, « Étoiles », « Le langage des schémas », « Le point fixe », Michel Serres se propose donc de nous faire prendre conscience que la liberté dans la composition des voies, déjà présente dans la philosophie de Leibniz, l’est aussi dans ses inventions au sein du modèle mathématique, affirmant que « partout dans son œuvre scientifique on reconnaît sa conscience aiguë des changements d’ordre, des variations et des restructurations ».

La thèse de Michel Serres, publiée en 1968.
La première partie (« Étoiles ») est consacrée aux multiplicités. D’abord les multiplicités représentatives : la méthode mathématique serait « un leurre vague ou un rêve géant » si elle ne se précisait pas en différents domaines (méthode géométrique, technique combinatoire, construction de séries, élaboration de quadratures…). Leibniz, nous dit l’auteur de cette thèse, a été le seul, parmi les savants de sa génération, à pouvoir approcher d’une certaine unité de la méthode mathématique, tout en multipliant les disciplines. Viennent ensuite les multiplicités historiques, puis les multiplicités monadiques : si, dans la philosophie de Leibniz, le monde est composé de monades, ce mot existe aussi dans ses mathématiques où la monade peut être l’unité en arithmétique ou le point en géométrie.
La deuxième partie (« Le langage des schémas ») explore d’abord dans la mathématique de Leibniz toute une « mathématique sagittale » (théorie des schémas, théorie des graphes…) imposant ses réseaux aux groupes humains eux-mêmes, qui empruntent aussi ces diagrammes. Elle s’attache ensuite aux « tables harmoniques » (tableaux, tables logiques, tables combinatoires…), que l’on retrouve aussi chez Leibniz. On passe enfin des modèles rigoureux de la mathématique, telle un dictionnaire parfait, au système philosophique, qui constituerait un lexique du même ordre : le cycle universel est bouclé.
La troisième partie (« Le point fixe ») termine l’ouvrage par les problèmes décisifs de la quête d’un point fixe et celle d’un référentiel, présentés à travers une analyse des travaux scientifiques de Blaise Pascal (1623–1662). Ce savant français, « initiateur de méthodes originales en géométrie, arithmétique, calcul et mécanique », les « transpose et les utilise visiblement dans la construction de son monde métaphysique ». C’est souvent que Michel Serres met Pascal en parallèle avec Leibniz. On comprend mieux, à la lecture de cet ouvrage, l’une des phrases de présentation par l’auteur du savant allemand : « Nos mathématiques naissent avec lui, nos sciences physiques sont prévues par lui, nos réseaux de communication, nos stocks de données, nos arts du signe et du langage sont déjà dans ses écrits. »
Les mathématiques, partout en filigrane
Michel Serres, tant dans ses écrits – dont certains, comme les Origines de la géométrie (Flammarion, 1993), relèvent franchement du domaine mathématique – que dans ses interventions médiatiques, n’est jamais loin des mathématiques ; c’est l’un des thèmes qu’il aborde volontiers. Dans l’un de ses derniers textes pour la presse, qui date de mai 2019 (Blaise Pascal, l’homme face à l’infini dans le hors-série 42 de Philosophie Magazine), le philosophe tisse une fois encore des liens entre Pascal et Leibniz, montrant comment ces deux savants « pensent en algorithmes ».
Serres nous fait remarquer que si Pascal propose pour son célèbre « triangle arithmétique » une recette de construction, Leibniz imagine, lui, son « triangle harmonique », symétrique, formé des inverses des termes de celui de Pascal. Si Pascal invente sa « pascaline », la première machine à calculer mécanique, Leibniz crée, lui aussi, une machine à calculer utilisant le principe de son « cylindre cannelé ». Tous deux ont donc, nous dit l’auteur de l’article, « contribué à une bifurcation complète et inédite dans l’histoire des mathématiques ».
Il ne manque pas non plus de rappeler (France-Info, dimanche 27 mai 2018), citant Galilée, selon lequel « le monde est écrit en langue mathématique », que ceux qui contribuent aux transformations techniques ou biologiques font basculer le monde et métamorphosent la société. Cette « bascule », il l’avait déjà présentée en rappelant sa jeunesse : « En philo à l’ENS j’ai passé deux ans […] à m’initier aux mathématiques dites “modernes”. Ma chance a été de voir se produire la bascule avec les maths que j’avais apprises. […] Je me suis aperçu qu’être mathématicien ou physicien, ce n’était pas savoir les maths mais avoir basculé […] et la bascule, c’est la pensée même. »
Michel Serres n’était pas non plus le dernier à défendre l’honneur des sciences en général, et des mathématiques en particulier, mettant toujours en avant le fait qu’elles transforment la société. Il le fait d’ailleurs avec adresse, « recadrant » sur France Info un ancien ministre qui avait cru bon de dire qu’à son avis les mathématiques ne servaient à rien. Il mettait au passage en évidence le manque criant de connaissances scientifiques de ceux qui nous gouvernent, insistant sur l’opposition entre « les incultes savants » (les scientifiques) et les « cultivés ignorants » (les littéraires), et énonçait clairement que les mathématiques, les « lois du monde » selon Einstein, sont pour lui « le comble de l’utilité ». Essayons de ne pas l’oublier.

Les premières lignes du triangle arithmétique de Pascal.
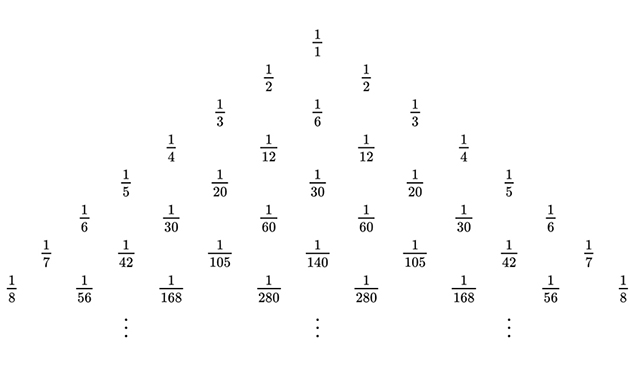
Les premières lignes du triangle harmonique de Leibniz.
Lire la suite