
L’origami et, plus généralement, les techniques de pliage d’une feuille de papier donnent lieu à de belles excursions dans le monde de la géométrie, de la topologie et de la combinatoire (voir notre dossier « La mathématique du pliage » dans Tangente 146, 2012). Si l’on enrichit la panoplie des opérations permises, par exemple en s’autorisant à couper la feuille de papier, quelles perspectives nouvelles s’ouvrent ? Le cas des cartes animées (ou pop-ups en anglais) est à lui seul déjà riche d’enseignement et offre des pistes de recherche originales et abordables pour tous les amateurs de belle géométrie.
Heaume sweet heaume
L’ingénieure Stephanie Jakus et le mathématicien Joseph O’Rourke se sont intéressés à une carte particulière. Avant de démarrer, il convient de savoir faire la distinction entre un pli vallée et un pli montagne. Dans le premier cas, la droite portant le pli peut servir de support (instable) à la feuille ; on le note schématiquement avec une ligne discontinue. Dans le second cas, le pli forme une crête ; on note avec une alternance de traits et de points.
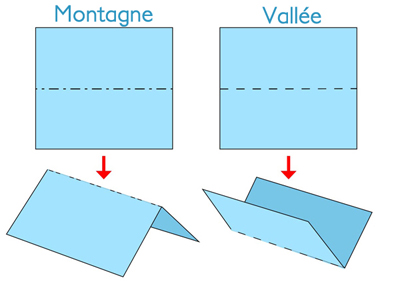
Le pli vallée et le pli montagne.
Pour construire la carte de Jakus et O’Rourke, on commence par plier la carte en deux volets à l’aide d’un pli vallée. Au milieu, on dessine un cercle. Dans l’espace délimité par le cercle, on découpe des fines bandes de papiers, perpendiculairement au pli. À l’ouverture de la carte (on note α l’angle d’ouverture), si l’on replie ces bandes de papier vers l’extérieur à l’aide d’un pli montagne le long du diamètre (précisément là où passe le pli vallée), on obtient une figure ressemblant à la visière d’un heaume. Les deux comparses se sont alors demandé quelle était la nature de la courbe obtenue au niveau de l’arête de la visière dans un plan médian des deux faces de la carte.

Le découpage et les plis de la visière du heaume.

L’arête de la visière dessine une courbe.

La carte animée est constituée de deux morceaux de plan : le volet inférieur en brun et le volet supérieur en bleu ciel, qui fait un angle α avec le précédent.
En bleu foncé se trouve le plan médian.
Quand la carte est complètement ouverte (α = 180°), ses deux volets reposent sur le même plan ; la courbe décrite par l’arête de la visière est un segment de droite, à savoir le diamètre du cercle de départ ( Γ ).
Une courbe inattendue
Voyons le cas où la carte est complètement fermée (α = 0°). Les volets supérieur et inférieur se superposent. À cause du pli au niveau du cercle ( Γ ), la bandelette qui était en [AB] quand α valait 180° se retrouve en [BC], avec C sur l’arête et AB = BC. La tangente au cercle (Γ) en B se trouve alors être la bissectrice de l’angle
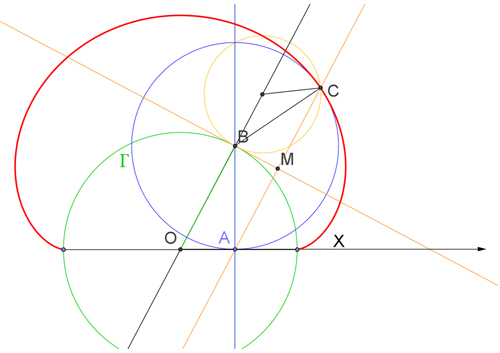
La figure obtenue lorsque α = 0°.
Si le cercle ( Γ ), en vert sur le schéma, est de rayon 1 et de centre O pris comme origine, considérons un axe des abscisses (Ox) dirigé par le pli de la feuille. Un axe des ordonnées (Oy) est choisi de manière à constituer un repère (x O y) orthonormé.
Calculons l’image d’un point A(s, 0) situé sur le pli, à l’intérieur de ( Γ ), avec –1 ≤ s ≤ 1.
Le point B est sur le cercle d’équation
donc a pour coordonnées
La tangente en B au cercle (Γ) est perpendiculaire au rayon [OB], c’est donc la droite d’équation
Maintenant, le point C est l’image du point A par réflexion par rapport à cette droite.
La droite (AC) étant perpendiculaire à la tangente en B au cercle (Γ), sa pente est égale à
L’équation de la droite (AC) est donc
Le milieu M du segment [AC] se trouve d’une part sur la droite (AC) et d’autre part sur la tangente en B au cercle ( Γ ). Les coordonnées ( xM, yM ) de M sont donc solutions des équations de ces deux droites. Tous calculs effectués, on trouve :
xM = s ( 2 – s 2 ),
yM = (1 – s 2 )3/2.
On en déduit les coordonnées ( xC , yC ) du point C :
xC = s ( 3 – 2 s 2 ),
yC = 2 (1 – s 2 )3/2.
La courbe décrite par C lorsque A se promène sur le diamètre du cercle ( Γ ) est donc, par définition, une néphroïde (en rouge sur le schéma) ! C’est aussi la courbe obtenue par la rotation d’un cercle de rayon 1/2 sur le cercle ( Γ ) : sur le schéma, le cercle orange roule sans glisser sur le cercle vert et le point C, fixe, décrit la courbe en rouge (voir aussi les dossiers « Les lieux géométriques » dans Tangente 176, 2017 et « Courbes planes » dans Tangente 125, 2008).
La néphroïde est également l’enveloppe des cercles dont le centre se trouve sur le cercle ( Γ ) et qui sont tangents au pli de la feuille (sur le schéma, regardez le cercle bleu, de centre B : il est tangent à l’axe des abscisses, donc au pli vallée de la feuille).
En route vers l’espace
Intéressons-nous maintenant au volet inférieur, supposé fixe dans le plan (x O y ). Le volet supérieur fait maintenant un angle α, strictement compris entre 0 et 180°, avec le plan précédent. Pour des raisons de symétrie, l’arête se trouve dans le plan médian, celui qui réalise un angle α / 2 avec le volet inférieur. Cherchons à caractériser la courbe qui représente le lieu des points de l’arête lorsque α varie de 0 à 180°.
Tout point P ( x P , y P , z P ) de l’arête est relié au cercle, sur le volet inférieur, par une lamelle de longueur R en un point B de ( Γ ). Ce même point P est aussi relié au cercle, sur le volet supérieur, par une bandelette de longueur R en un point B1 de ( Γ ). Ainsi, P appartient à un cercle (Δ) du plan médian, intersection de deux sphères centrées en B et en B1.
À cause du pli tangent au cercle (Δ), l’angle en tout point de l’arête entre les deux lamelles de la bandelette de papier sera toujours le même. On en déduit qu’un point P de l’arête va parcourir, lors de la rotation du volet supérieur, un demi-cercle perpendiculaire au plan du volet inférieur. Ce demi-cercle, en rouge sur la figure suivante, se trouve dans un plan ( Π ) perpendiculaire au plan (x O y) et passe par A et C. Un point de la courbe cherchée est donc l’intersection de deux sphères, du plan médian et de ce dernier plan vertical ( Π ).
Ses coordonnées dépendent par ailleurs de l’abscisse s fixée (comprise entre –1 et 1) et de l’angle α considéré (compris entre 0 et 180°).

Les différentes courbes obtenues pour α compris entre 0° et 170°.
Tous calculs faits, on obtient :
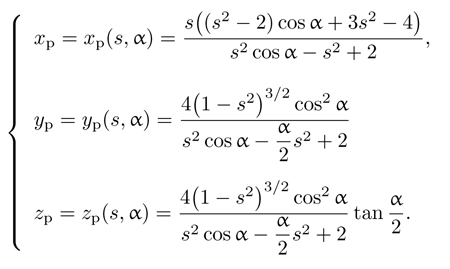
L’amateur de géométrie reconnaît bien là, dans tous les cas, les équations de néphroïdes. Ainsi, en partant d’un cercle sur notre carte animée, on obtient une néphroïde.
De la parabole au cercle

En brun, la parabole du volet inférieur.
En bleu, les arcs de cercle obtenus pour α compris entre 0° et 170°.
À l’inverse, de quelle courbe doit-on partir sur le pop-up pour obtenir, à partir de nos bandelettes de papier, un arc de cercle lors de l’ouverture du volet de la carte ? Quelques expérimentations suffisent à se convaincre qu’il faut partir d’une parabole. Cela se démontre analytiquement. Notre ami François Lavallou nous a cependant proposé une très jolie démonstration, purement géométrique.
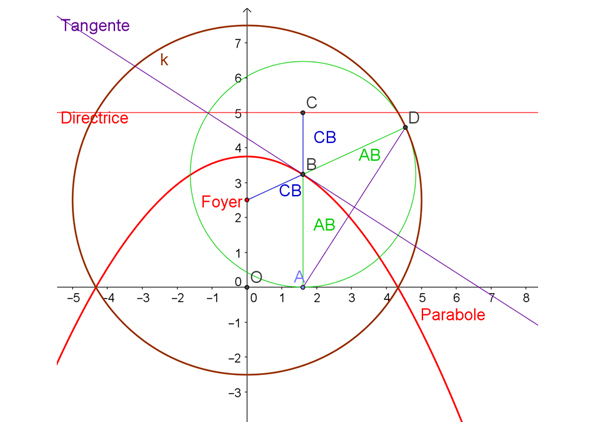
La courbe de départ est une parabole (en rouge) définie par un point privilégié, le foyer, et une droite appelée directrice. Pour une bandelette de papier [AB] perpendiculaire à la directrice, la longueur AC est constante. La droite (AC) coupe la parabole en B. La droite [AB] se reflète dans une droite passant par le foyer. Le point D définit un cercle dont le centre est le foyer de la parabole et dont le rayon est AC.
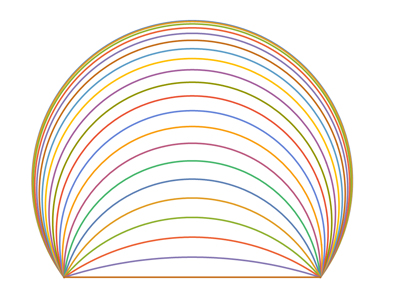
La projection des différents arcs de cercles obtenus.

Le découpage et les plis suivant une courbe de départ constituée de deux arcs de parabole.

Pour un angle donné, l’arête dessine bien un cercle dans le plan médian.
Un calcul similaire montre que pour des angles différents de 0° on obtient des cercles dans le plan médian. C’est un théorème original que nous avons démontré.
À votre tour maintenant d’essayer d’autres courbes pour les plis initiaux ! Trouver une formule générale permettant de trouver la forme (et les équations) du pli initial en fonction de la courbe que l’on souhaite obtenir ne paraît pas trivial, mais qui sait… Un lecteur inspiré saura peut-être relever le défi.
Lire la suite