Le mathématicien belge Jean Mawhin (né en 1942) affirme que « la modélisation mathématique est un art difficile, proche de celui du caricaturiste. Il faut obtenir un maximum de ressemblance en un minimum de traits. Il faut savoir négliger a priori ce qui sera a posteriori négligeable ». C’est souvent vrai. Mais qu’en est-il dans le domaine de la physique ? L’adéquation de plus en plus fine des modèles existants aux observations fait que, pour certains scientifiques, le modèle devient une expression alternative de la réalité. Les deux objets se confondent dans leur esprit pour devenir deux expressions équivalentes du même phénomène. Le modèle permettrait d’atteindre une certaine forme de réalité. Est-ce vraiment le cas ? Certes, la sophistication accrue de nos représentations mathématiques du réel livre des résultats de plus en plus conformes à ceux observés, avec une précision toujours croissante. Nos modèles s’améliorent. En sont-ils pour autant arrivés à une sorte de « perfection », quoi que l’on mette derrière ce terme ? Une réflexion sur la notion même de modèle s’impose…

Renoncer à l’exhaustivité

Si l’on suit l’historien des sciences italien Giorgio Israël (1945–2015), on peut nommer « modèle mathématique » « toute forme de description mathématique d’une classe de phénomènes ». Le modèle consiste en une construction mathématique ayant pour objectif de représenter, en prenant en compte certaines caractéristiques pertinentes et l’ensemble des données disponibles, un certain aspect de la réalité. En physique, on peut considérer avoir compris un phénomène lorsque l’on est à même d’en produire une représentation mathématique non contradictoire sous forme hypothético-déductive, les hypothèses prenant forme de « lois », qui en donne une description synthétique dont l’application calibrée produit des résultats ne s’écartant « pas trop » des observations.

L’histoire des sciences nous montre que la grande majorité des modèles possèdent des propriétés communes. Un modèle mathématique est une représentation fonctionnelle d’un élément de réalité au moyen d’objets abstraits appartenant au monde des mathématiques. Il est aussi une représentation sélective de la réalité. Pour le mettre en œuvre, le scientifique ne retient que certaines caractéristiques de la situation étudiée, pour en ignorer d’autres. Ce faisant, il renonce à l’idée d’aboutir à une image exhaustive de la réalité. Le modèle mathématique peut être également une représentation universelle : une même équation peut être à même de décrire adéquatement plusieurs phénomènes distincts. 

Ainsi l’équation différentielle \( \dfrac{d^2y}{dx^2} + ky = 0\)  s’applique aussi bien au mouvement d’une masse placée à l’extrémité d’un pendule lorsqu’elle est écartée de son point de repos qu’à celui d’un ressort légèrement étendu, ou encore, plus généralement, à la trajectoire de tout phénomène périodique correspondant au cas où la force considérée (égale au produit de la masse par l’accélération, soit la dérivée seconde de la fonction de déplacement) est supposée proportionnelle à ce déplacement. Un modèle peut alors être vu comme un fragment de mathématiques permettant d’unifier toute une catégorie de phénomènes, qu’il peut représenter indifféremment. En fait, chaque situation peut être analysée à travers différents modèles, et chaque modèle peut s’appliquer à différentes situations.

Enfin, un modèle est le plus souvent (et historiquement) une représentation évolutive. Tout modèle se construit à partir d’hypothèses. En première approche, la tentation est grande de simplifier ces hypothèses au maximum, afin d’obtenir le modèle « le plus élémentaire possible », dans le cadre d’un principe de parcimonie (plus connu sous le nom de rasoir d’Occam). Chaque fois que le besoin s’en fait sentir, il convient d’affiner le modèle, par petites touches successives, en modifiant les hypothèses de manière à obtenir un outil de plus en plus sophistiqué, et de plus en plus conforme aux attentes. La question demeure : cette représentation progressive peut-elle à terme s’avérer non sélective ?

Des représentations mentales

Pour qu’une représentation mathématique d’une réalité physique soit acceptée provisoirement, il faut qu’elle soit compatible avec l’ensemble des observations engrangées. Le philosophe Karl Popper exprime fort justement les fondements de cette attitude scientifique : « La science se compose de théories qui sont notre œuvre. Nous construisons des théories, nous allons vers le monde avec nos théories. Mais le monde ne nous livre aucune information si nous n’allons pas vers lui en l’interrogeant : nous demandons au monde si telle ou telle théorie est juste ou est fausse. Ensuite nous soumettons ces questions à l’examen le plus approfondi possible sans jamais parvenir à aucune certitude. » Le fait, pour un modèle, d’avoir été validé par un très grand nombre d’expérimentations n’implique pas obligatoirement qu’il soit une « bonne » description de la réalité, mais c’est une condition nécessaire à son utilisation. Cependant, une seule expérience additionnelle pourra le mettre en défaut.

On observe aussi que la modélisation d’un phénomène complexe est rarement unique. Il peut exister plusieurs modèles issus d’une théorie générale, basés sur des prémisses différentes, tous compatibles avec les observations. C’est le cas notamment en ce qui concerne les modèles cosmologiques, fort nombreux aujourd’hui, parfois contradictoires, et dont aucun ne fait l’unanimité auprès des scientifiques.

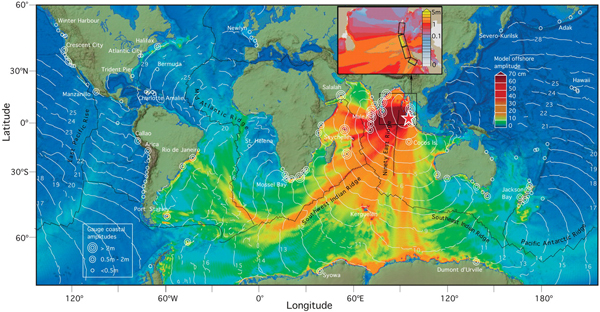
Modélisation mathématique des tsunamis, 
ici simulation du tsunami de décembre 2004 (Sumatra) 
© http://images.math.cnrs.fr/Modelisation-mathematique-des.html

Intéressons-nous enfin à la structure même du modèle : les mathématiques ! On sait que toutes les axiomatiques mathématiques consistent en une série d’hypothèses d’existence d’objets (non définis) et de relations entre ces objets. Ces axiomatiques présentent donc une structure totalement analogue à celle de notre cerveau constitué de neurones (objets non définis) reliés entre eux au moyen de synapses (relations). Qu’on le veuille ou non, nos mathématiques sont fondamentalement ancrées dans notre réalité d’humains. Elles nous permettent d’imaginer et de manipuler des objets non réels. Une sphère n’existe pas dans le monde réel. Mais nous pouvons nous en faire une représentation mentale. Nous pouvons également utiliser le concept de sphère pour nous représenter des objets réels moins réguliers, plus complexes que la sphère. Mais cette constatation en impose une autre : un modèle mathématique d’une réalité physique n’est jamais que ce que notre cerveau peut s’en faire comme représentation. Sa complexité est limitée par celle de nos réseaux neuronaux. Et qui oserait affirmer que la structure de nos cerveaux est suffisamment élaborée pour arriver à la compréhension globale de notre univers ?