près une formation de médecin, Hermann Ludwig Ferdinand von Helmholtz (1821–1894) s’est tourné vers les mathématiques et les sciences physiques, et a ainsi pu étudier les phénomènes sonores sous l’angle de la physique, de leur modélisation mathématique, mais aussi comme un phénomène perçu par un organisme vivant. Son livre Théorie physiologique de la musique (Masson, 1868) a largement marqué les esprits de son époque. Helmholtz s’intéressait en effet avant tout aux sons musicaux en caractérisant trois paramètres essentiels en musique : l’intensité, la hauteur et le timbre.

Les caractères du son

Pour un son donné, la hauteur est son caractère grave ou aigu et correspond à une fréquence de vibration de l’air. Le physicien Joseph Sauveur (1653–1716) est considéré comme le fondateur de l’acoustique scientifique. Il a systématisé des expériences consistant à remarquer que, sous l’influence d’un son, les cordes libres d’un instrument correspondant à la fréquence de ce son se mettaient spontanément en vibration, mais qu’il en était de même des cordes (en rouge dans le schéma) ayant des fréquences de vibration naturelles doubles, triples (ou autres multiples entiers) de cette fréquence.

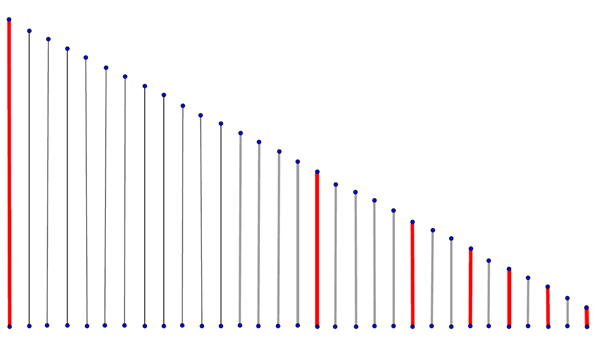
Cordes libres vibrant sous l’influence d’un son : seules vibrent celles dont la fréquence est un multiple de la fréquence fondamentale du son.

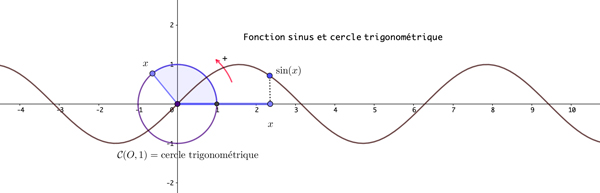
Dans la lignée des observations de Pythagore (VI ^e siècle avant notre ère), René Descartes et Isaac Beeckman (XVII ^e siècle), cela a conduit Sauveur à une théorie selon laquelle tout son possédant une hauteur était composé de sons ayant des fréquences multiples de celle qui caractérise cette hauteur. Les travaux de Sauveur laissent entrevoir que l’on peut connaître la totalité des paramètres d’un son si l’on connaît sa décomposition en ce que l’on a appelé alors les sons purs qui le composent, et cela inclut donc les caractères distinctifs du son (son timbre). Les sons purs sont de fréquences multiples de la fréquence  f de base, appelée son fondamental. Les autres fréquences présentes sont appelées les harmoniques. On a assez vite pensé que les sons pouvaient être décrits par les fonctions sinusoïdales, reliées (par définition) à la position d’un point se déplaçant à vitesse constante sur un cercle.

Lorsque, pour résoudre des problèmes de nature complètement différente, Joseph Fourier (1768–1830) a montré que l’on pouvait approcher « presque parfaitement » nombre de fonctions périodiques à l’aide de sinusoïdes ayant une même fréquence commune ou des fréquences multiples, ce résultat a été très rapidement interprété en termes d’acoustique. Helmholtz a alors émis l’hypothèse que le timbre d’un son était caractérisé par la « forme » de la fonction, et plus précisément par les intensités relatives de chaque son pur. Il suffisait alors de connaître l’amplitude de vibration de chaque composante d’un son composé pour connaître son intensité globale, sa hauteur et son timbre à un instant donné. Le diagramme qui rassemble ces renseignements à un temps t donné est appelé spectre du son.

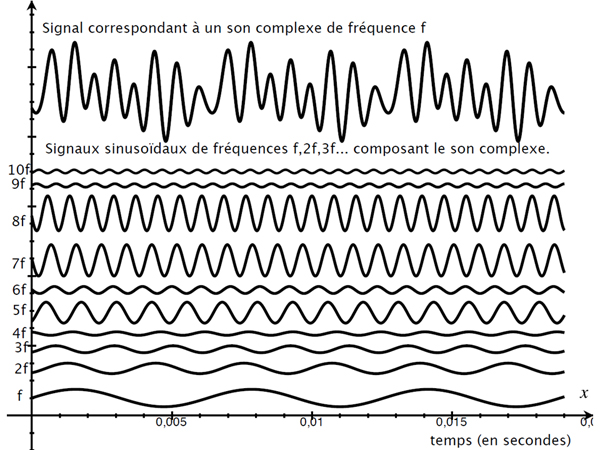
Décomposition de Fourier d’un signal périodique.

La théorie de Helmholtz a eu un grand retentissement. Elle a ouvert en physiologie un champ nouveau en portant l’étude de la perception au-delà des organes purement externes ; elle a contribué au développement de la théorie du signal, aujourd’hui indispensable à la plupart des ingénieurs. En ce qui concerne les musiciens, elle a permis de proposer des explications de phénomènes anciens, comme la dissonance ou les interférences.

L’approche de Helmholtz a dû cependant être complétée, notamment son étude du timbre. Il s’est intéressé aux sons représentés mathématiquement par des fonctions périodiques et a effectué ses vérifications sur les voyelles de la langue, sons pour lesquels cette approche est en effet assez satisfaisante. Toutefois, l’attaque des sons (le crissement d’un archet sur une corde, le bruit lié au pincement d’une corde, un choc sur un xylophone…) joue un rôle essentiel dans la perception du timbre ; la succession des évènements sonores sur de très petites durées est également importante. Ainsi, selon les phénomènes étudiés, il convient de pouvoir représenter non seulement les amplitudes de chaque composante d’un son, mais également leur durée, voire leur développement au cours du temps.

La représentation des composantes non périodiques d’un son a également été rendue possible par une généralisation de la théorie de Fourier. En effet, les sons peuvent être représentés comme un continuum de fréquences, plus ou moins concentrées autour de certains pôles. Ainsi, la lecture des diagrammes utilisés est plus complétée qu’invalidée par cette nouvelle approche. Mais une analyse fine d’un son ne saurait se faire à l’aide seulement d’un nombre relativement petit de données, et donc de calculs.

La musique spectrale

En parallèle avec le laboratoire d’acoustique musicale de l’université de Jussieu (Paris-VI) fondé par Émile Leipp (1913–1986), les pratiques musicales des musiciens contemporains ont pris en compte cette possibilité de modélisation. L’usage de sons non conventionnels en musique occidentale (par exemple certains instruments de percussions exotiques) s’est vu complété par un travail sur les sons eux-mêmes. Le travail sur bande magnétique a été suivi d’un travail direct sur ordinateur. Cela a permis de caractériser le timbre de chaque instrument classique de manière très précise, et ainsi d’apporter des éléments nouveaux en termes d’orchestration.

Le fonctionnement de l’oreille interne étant mieux compris, on approfondit désormais l’étude de la psychologie de l’audition. Les sons des instruments ont pu également être retravaillés de manière électronique avant d’être amplifiés, afin de créer des effets divers, de distorsion ou de spatialisation typiquement.

Enfin, l’ordinateur a pu devenir lui-même un instrument capable d’« imiter » certains instruments de musique ou d’en « créer » d’autres. Les compositeurs contemporains conçoivent même souvent des œuvres pour lesquelles des capteurs se trouvent au sein de l’orchestre ou d’un instrument et interagissent en direct avec les sons produits (en créant des effets d’échos déformés ou de brouillard sonore…).

Ce point de vue, d’abord défendu par les compositeurs d’un courant appelé la musique spectrale, en référence au spectre de Fourier qui décrit scientifiquement les sons, fait désormais partie de la formation de nombreux compositeurs. En France, l’Institut de recherche en coordination acoustique–musique (Ircam), une institution phare dans ce domaine au niveau international, lui consacre une part très importante et permet à des chercheurs et compositeurs d’horizons très divers de se rencontrer et de faire évoluer ces idées.