Nombres complexes et trigonométrie

En 1748, alors qu'il dirige la classe de mathématiques de l'Académie de Berlin, Leonhard Euler publie en latin un ouvrage remarquable et qui fera date, sous le titre Introductio in Analysin infinitorum. Cette Introductio rompt l'ancrage du calcul différentiel dans les figures géométriques qui donnaient jusque-là sens et consistance aux outils de calcul. Pour cela, Euler va inverser l'ordre d'exposition habituel et la hiérarchie des disciplines : il va développer d'abord dans un premier volume le calcul des quantités numériques et algébriques par l'intermédiaire de l'étude des fonctions, avant d'aborder, dans un second volume, les questions de géométrie. Cette inversion lui permettra de dégager les relations purement numériques entre des fonctions trigonométriques définies jusque-là de manière géométrique avec la fonction exponentielle et les nombres complexes.

Les formules d'Euler

Après avoir déterminé les développements en série des principales fonctions classiques de l'analyse, Euler donne les célèbres formules qui portent son nom (x désigne un réel quelconque) :

   \( e^{ix}=\cos x + i\sin x, \)     \( \cos x = \dfrac{e^{ix} + e^{-ix}}{2},\)  

\( \sin x = \dfrac{e^{ix} - e^{-ix}}{2i}\)       \( \tan x=\frac{\cos x}{\sin x}=\frac{1}{2}\frac{e^{ix}-e^{-ix}}{e^{ix}+e^{-ix}}\)  

\( e^{ix}+1=0\) .

Cette dernière est qualifiée par certains de « plus belle formule mathématique » en ce qu'elle réunit, en une seule relation, les cinq nombres les plus importants de l'analyse.

Les diverses formules trigonométriques circulaires ne sont alors que la traduction des propriétés des exponentielles imaginaires, comme e⁰ = 1, e^inx = (e^ix)ⁿ , e^iu e^iv = e^i(u+v) … Par exemple, la deuxième égalité traduit la célèbre formule de Moivre (cos x + i sin x)ⁿ = cos(nx) + i sin(nx), pour n un entier quelconque. Elle permet de calculer cos(nx) et sin(nx) en fonction des puissances de cos x et sin x grâce à la formule dite du binôme de Newton.

Fort de ces relations, Euler s'en donne alors à cœur joie pour calculer toutes sortes de développements en séries, entières ou numériques, sans toujours se préoccuper de leur convergence, ni de leur extension possible aux nombres complexes. Ainsi, ayant obtenu d'une part l'égalité 

  \( z=\dfrac{1}{2i}\ln\dfrac{\cos z+i\sin z}{\cos z-i\sin z}= \dfrac{1}{2i}\ln\dfrac{1+i \tan z}{1-i \tan z}\)

et d'autre part la série

  \( \ln\dfrac{1+x}{1-x}= \dfrac{2x}{1}+ \dfrac{2x^3}{3}+ \dfrac{2x^5}{5}+ \dfrac{2x^7}{7}+...,\)

il obtient, en remplaçant, dans la série, x par i tan z :

  \( z= \dfrac{\tan z}{1}- \dfrac{(\tan z)^3}{3}+ \dfrac{(\tan z)^5}{5}-\dfrac{(\tan z)^7}{7}+...\)  

Ou encore, en posant t = tan z :

\( \arctan t = \dfrac{t}{1} - \dfrac{t^3}{3} + \dfrac{t^5}{5} - \dfrac{t^7}{7} + ...\)  

retrouvant avec t = 1 la célèbre formule de Leibniz :

\( \dfrac{\pi}{4} = 1 - \dfrac{1}{3}+ \dfrac{1}{5}- \dfrac{1}{7} + ...\)  

Dans l'Introductio, Euler établit aussi des décompositions en produits infinis pour des expressions, comme :   

Mais il ne nomme ni n'étudie ces fonctions à part, alors qu'il donne également les développements similaires pour les fonctions circulaires : 

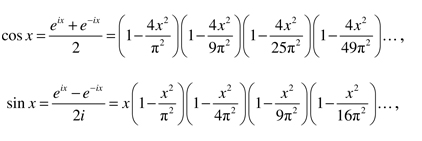
conforté par le fait que ces développements s'annulent lorsque 

\( x = \dfrac{2k +1}{2}\pi\)   ou  \( x = - \dfrac{2k +1}{2}\pi\)

pour le cosinus, et \( x = k\pi\) ou \( x = -k\pi\)  pour le sinus (k un entier relatif).

 
Les fonctions hyperboliques

C'est en 1757 que le mathématicien italien Vincenzo Riccati (1707–1775), cherchant à calculer l'aire sous l'hyperbole équilatère d'équation x² – y² = R², introduit les fonctions hyperboliques, par analogie avec les fonctions circulaires.

Comme pour le cercle, paramétrons les coordonnées d'un point M de l'hyperbole équilatère (H), limitée à x ≥ 1, d'équation x² – y² = 1, par (x = ch  \( \alpha\) , y = sh  \( \alpha\) ), où ch désigne le cosinus hyperbolique et sh le sinus hyperbolique. Mais quel sens donner à l'argument  \( \alpha\)  ? Peut-on le considérer comme un angle, et si oui lequel ? Poursuivons l'analogie avec le cercle…

Dans le cas de l'hyperbole, l'aire S du secteur AOM pour un point M d'abscisse x ≥ 1 et d'ordonnée  \( y = \sqrt{x^2-1}\) est mesurée par :

En posant, par analogie aux fonctions circulaires, cette aire égale à  \( \alpha/2\) , on obtient :

\( x+\sqrt{x^2-1}=e^\alpha,\)   \( x-\sqrt{x^2-1}=e^{-\alpha},\)

d'où l'on déduit les formules classiques

\( \text{ch} \;{\alpha} =\dfrac{e^\alpha + e^{-\alpha}}{2},\)   \( \text{sh} \;{\alpha} =\dfrac{e^\alpha - e^{-\alpha}}{2} \) et   \( \text{th} \;{\alpha} =\dfrac{e^\alpha - e^{-\alpha}}{e^\alpha + e^{-\alpha}} \)  

 (th pour tangente hyperbolique, th = sh / ch), où a mesure donc le double de l'aire S du secteur hyperbolique AOM.

Trigonométrie circulaire et hyperbolique.

Ainsi, la symétrie entre les exponentielles et les fonctions circulaires s'élargit en un nouveau domaine, la trigonométrie hyperbolique, avec un passage très simple de l'une à l'autre :

ch(u) = cos(iu), sh(u) = –i sin(iu),

ch(iu) = cos(u), sh(iu) = i sin(u), 

cos(u) = ch(iu) et sin(u) = – i sh(iu).

Alors, pour x et y réels :

sin(x + iy) = sin(x) cos(iy) + sin(iy) cos(x) = sin(x)ch(y) + i cos(x) sh(y)

et cos(x + iy) = cos(x) cos(iy) – sin(x) sin(iy) = cos(x)ch(y) – i sin(x) sh(y).

Examinons plus en détail la formule du sinus. Pour x variable, y = b fixé, le nombre complexe sin(x + ib) a pour image le point M de coordonnées (sin(x)ch(b), cos(x) sh(b)) et appartient à l'ellipse (E) d'équation X² / ch²(b) + Y² / sh²(b) = 1.

Pour y variable et x = a fixé, le nombre complexe sin(a + iy) a pour image le point N de coordonnées (sin(a)ch(y), cos(a)sh(y)) et appartient à l'hyperbole (H) d'équation X² / sin²(a) – Y² / cos²(a) = 1.

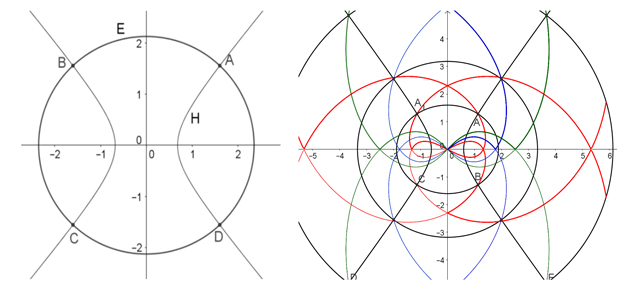
à gauche : sin (0,75 – 1,5 i ) = sin (0,75) ch (1,5) – i cos (0,75) sh (1,5) = 1,50 – 1,56 i a pour image le point D.

à droite :  Lignes de niveau de sin (a + i k a) pour k = 0,5 (en rouge), k = 1 (en vert) et k = 0,75 (en bleu).

L'image de sin(a + ib) est donc l'un des quatre points de la figure ci-contre, le choix entre les points se faisant selon les signes des parties réelles et imaginaires.

On peut aussi tracer des lignes de niveau correspondant à certaines relations entre a et b. Ainsi la figure ci-dessus correspond aux images de sin(a + ia / 2) (en rouge), de sin(a + ia) (en vert) ou encore de sin(a + 0,75a) (en bleu) lorsque a varie. Elles ont pour équations paramétriques x = sin(t) ch(kt) et y = cos(t) sh(kt) pour k = 0,5, 1 et 0,75 successivement.

 
Des applications à l'électricité

Arthur Edwin Kennelly (1861–1939), ingénieur en électricité américain, a montré que l'on pouvait généraliser les lois d'Ohm (établies d'abord pour les courants continus) aux courants alternatifs au moyen des nombres complexes. Beaucoup de phénomènes électriques, particulièrement ceux concernant les lignes téléphoniques et les réseaux combinant résistances, inductances et capacités (les circuits RLC), conduisent à des équations différentielles du second ordre, à coefficients réels constants, de la forme a x''(t) + b x'(t) + c x(t) = f (t).

Selon le signe du discriminant \( \Delta\)  de l'équation du second degré ar² + br + c = 0 (équation dite caractéristique), l'ensemble des solutions de l'équation sans second membre associée a x''(t) + b x'(t) + c x(t) = 0 sera donné par les fonctions suivantes (dans lesquelles A, B, M et w sont des réels quelconques) :

• x(t) = \( e^{\alpha t}\) (A ch( \( \beta\) t) + B sh( \( \beta" style="font-size: 10px;\) t)) dans le cas où \( \Delta\)  =  \( \beta^2\)  > 0 et où l'équation caractéristique a pour racines \( \alpha + \beta\)  et  \( \alpha - \beta,\)

• x(t) = (At + B) \( e^{\alpha t}\)  dans le cas où  \( \Delta\)  = 0 et où l'équation caractéristique a pour racine double  \( \alpha\) ,

• x(t) =  \( e^{\alpha t}\) (A cos( \( \beta" style="font-size: 10px;\) t) + B sin( \( \beta" style="font-size: 10px;\) t)) =  \( e^{\alpha t}\)  M cos( \( \beta" style="font-size: 10px;\) t + \( \phi\) ) dans le cas où  \( \Delta\)  < 0 et où l'équation caractéristique a pour racines complexes conjuguées \( \alpha + i \beta\)  et  \( \alpha - i \beta\) .

 

En fait, les première et troisième situations, apparemment distinctes, peuvent se traiter sous une même rubrique en généralisant la notion d'angle dans deux directions : en introduisant les angles hyperboliques ; en définissant les angles complexes. De cette manière, les fonctions définies par cos( \( \alpha\) ) et sin( \( \alpha\) ) sont obtenues par les exponentielles \( e^{i\alpha}\) et \( e^{-i\alpha}\) , caractérisées par l'angle circulaire  \( \alpha\) .

Celles définies par ch( \( \theta\) ) et sh( \( \theta\) ) sont obtenues par les exponentielles \( e^\theta\)  et \( e^{-\theta}\)  et caractérisées par l'angle hyperbolique  \( \theta\) .

Aux fonctions définies par \( e^\theta \cos( \omega)\)  et \( e^\theta \sin( \omega)\) , qui sont en fait obtenues par les exponentielles \( e^{\theta + i \omega}\)  et \( e^{\theta - i \omega}\) , on associera par convention les angles complexes conjugués  \( \theta\)  + i \( \) \( \omega\)  et  \( \theta\)  - i \( \) \( \omega\) , ainsi que leurs cosinus et sinus (au choix, « hyperboliques » ou « circulaires » car leur distinction n'a plus de raison d'être : les propriétés de l'exponentielle permettent de passer de l'une des formes à l'autre).

À une époque où il n'y avait pas encore de calculatrice électronique, Kennelly a calculé et tabulé, à une précision de 10^–5, les fonctions circulaires et hyperboliques des nombres complexes x + iq par intervalles de 0,05. Il a aussi constitué un atlas de trente-deux graphiques facilitant les interpolations.

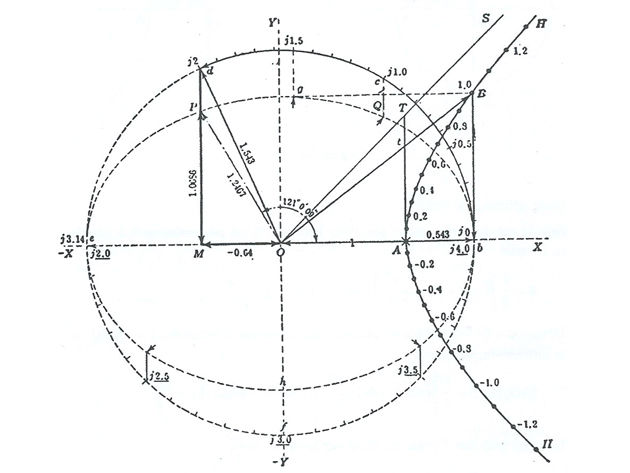
À titre d'exemple, voyons une construction graphique de ch(1 + 2i) et, plus généralement, de ch(1 + i  \( \omega\) ) pour tout réel  \( \omega\) . Les axes de coordonnées (OX) et (OY) sont les axes d'une hyperbole équilatère HABH' dont (OS) est une asymptote. La distance OA sur l'axe (OX) étant prise pour unité, les points 0,2, 0,4, 0,6… sur l'hyperbole indiquent les arcs correspondant aux angles hyperboliques de 0,2 radian hyperbolique, 0,4 radian hyperbolique, 0,6 radian hyperbolique…

Pour avoir la valeur de ch(1 + 2i), on utilise la formule d'addition et les formules précédentes (passage hyperbolique–circulaire). Menons la perpendiculaire (bB) à (OX) où B correspond à un angle hyperbolique de 1 radian. Donc bB mesure sh(1) et Ob mesure ch(1). De O comme centre et Ob comme rayon, traçons le cercle bcdef et délimitons sur ce cercle l'arc \( \overset{\frown}{bd}\)  , qui mesure 2 radians circulaires. Enfin, depuis d, abaissons la perpendiculaire (dM) sur l'axe (OX) et faisons l'affinité de rapport th(1) = bB / Ob, qui transforme M en P et le cercle en une ellipse (E). Alors  \( \overrightarrow{OP}\) est l'image vectorielle complexe de ch(1 + 2i) : 

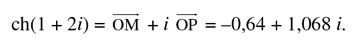
Les valeurs de ch \( (1+ i\omega)\)  sont alors immédiatement accessibles à partir de l'ellipse. Par exemple, ch(1 + i) sera donné par  \( \overrightarrow{OQ}\) et ch(1 + 1,05 i) par \( \overrightarrow{Og}\) .

Les ouvrages de Kennelly expliquent comment ces angles généralisés sont appliqués à l'ingénierie électrique. Leur utilisation a augmenté à l'extrême la puissance du calcul ! Inversement, le génie électrique a fécondé en profondeur deux domaines des mathématiques pures, les nombres complexes et la trigonométrie généralisée des fonctions hyperboliques et circulaires.