Le problème 197 de la rubrique « Affaire de logique » du journal Le Monde, intitulé À la pointe du triangle, en est un exemple. On y fabrique un triangle numérique d'ordre 5 où chaque nombre est obtenu en additionnant les deux nombres de la ligne supérieure entre lesquels il est placé :

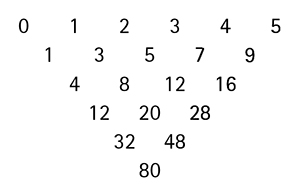
Sauriez-vous calculer, de préférence mentalement, le nombre à la pointe d'un tel triangle, mais d'ordre 6 ? Et, sans le construire, donner un ordre de grandeur de celui de la pointe d'un triangle d'ordre 20 ? 

Un autre exemple, mais sans chiffres cette fois, est le problème 281 de cette même rubrique. On fabrique ici des tableaux triangulaires de signes « + » et « – » en écrivant sous chaque couple de signes le résultat d'une multiplication, selon l'habituelle règle des signes :

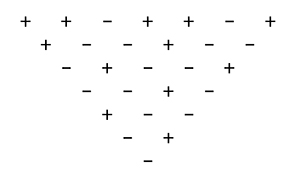
La question est maintenant de trouver quels signes doivent figurer sur la première ligne pour que le tableau complet contienne autant de signes + que de signes –. Une jolie énigme, non ?

Les réponses se trouvent ci-après, mais consultez-les uniquement après avoir cherché !

Solutions : des lecteurs inventifs

À la pointe du triangle d'ordre 6 se trouvera 192. Il suffit, pour le trouver, de remarquer que les lignes constituent des suites arithmétiques, de raisons successives, par ligne : 1, 2, 4, 8, 16, puis 32 sur la cinquième. Ses premiers nombres seront donc 80 et 112, d'où le résultat 192 à la pointe.

Quant à la pointe du triangle d'ordre 20, elle vaut 20 × 2¹⁹ = 10 × (1 024)² soit environ 10 × 1 000² ou encore 10⁷. On peut en effet montrer que le premier terme de la ligne p + 1, qui est aussi la pointe du triangle d'ordre p, est précisément p × 2^p–1.

Pour la seconde énigme, les lecteurs de la rubrique ont été très inventifs ; certains ont mis en évidence à la main toutes les solutions. Voici leurs premières lignes : deux sont symétriques par rapport à un axe vertical, cinq ne le sont pas.

Deux solutions « symétriques »  trouvées par les lecteurs du quotidien Le Monde.

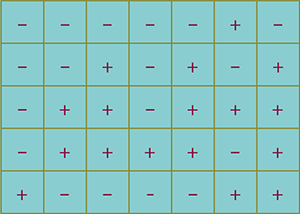
Les cinq solutions non symétriques.