Il n'est pas rare de constater que les « vrais découvreurs » d'objets ou de théorèmes mathématiques sont passés à la trappe de l'histoire. Il faut parfois les travaux approfondis d'historiens des sciences pour rétablir un peu de vérité… C'est manifestement le cas pour le « triangle de Pascal », dont la découverte précède le mathématicien et philosophe français de plus de dix siècles…
Inde : un courant de pensée favorable
Les travaux récents de Radha Gupta ont permis de remettre à l'honneur la science indienne. Un mathématicien indien du VIe siècle nous intéresse particulièrement : Varāhamihira. Les écrits de ce dernier ont fait l'objet d'une analyse détaillée dans le Ganita Bharati, le bulletin indien d'histoire des mathématiques (volume 14, 1992). Gupta nous y révèle que l'école Jaina de mathématique indienne portait un grand intérêt aux notions de permutations et de combinaisons, et que ce sujet aurait été étudié dès le IIIe siècle avant notre ère. Cette école est issue du jaïnisme (du sanskrit jina, « victorieux du soi », une philosophie religieuse datant du VIe siècle avant notre ère qui insiste sur le concept de non-violence et met l'accent sur l'ascétisme).
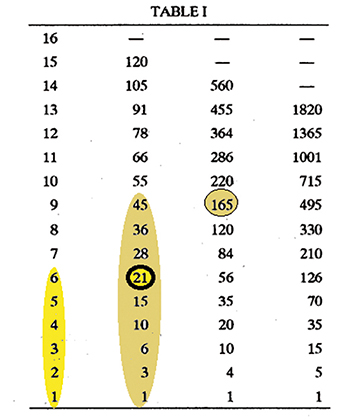
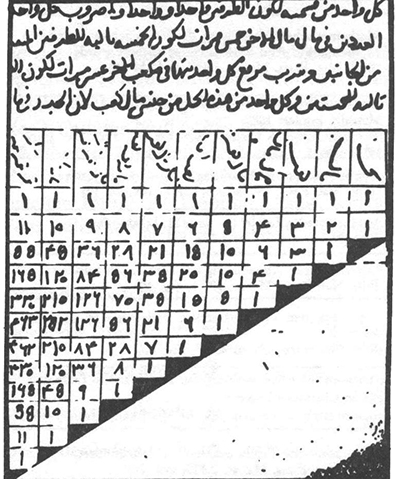
Les écrits de Varāhamihira proposent une construction originale d'un tableau de combinaisons dont le lien avec le triangle de Pascal est clair. La construction suit la règle suivante, énoncée en sanskrit par le savant : « En partant du bas de chaque colonne, et en additionnant tous les nombres situés plus bas, on obtient les combinaisons. » Les résultats de Varāhamihira sont présentés ci-contre. La colonne de gauche du tableau reprend la suite des entiers naturels. La colonne immédiatement à droite reprend les sommes de toutes les valeurs inférieures de la colonne immédiatement à gauche. Ainsi, le 21 cerclé de noir est égale à la somme des six premiers entiers naturels. Le nombre 165, encadré également, est égal à la somme des neuf nombres du bas de la deuxième colonne mis sur fond beige.
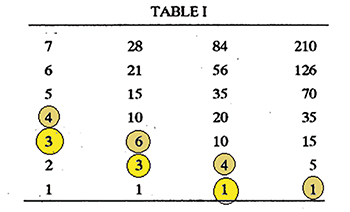
Si l'on regarde les nombres de la deuxième colonne, à partir du bas, on constate qu'ils représentent les combinaisons de deux nombres à choisir sans remplacement parmi n, soit la suite des nombres que l'on note aujourd'hui . On vérifie aussi que la troisième colonne donne la suite des . Les éléments du triangle de Pascal apparaissent donc sous la forme de diagonales, à cela près qu'il faudrait ajouter une première colonne de « 1 » à la gauche du tableau. En pratiquant ainsi et en utilisant toujours la règle de Varāhamihira, on obtient le triangle complet.
L'Inde est le trait d'union entre le monde arabe et le monde chinois. Il n'est pas étonnant de voir apparaître des concepts similaires dans ces deux régions du monde quelques siècles plus tard.
La construction d'un « triangle de Pascal » dans la sphère arabo-musulmane serait à attribuer au mathématicien persan Abu Bakr Muhammad ibn al-Hasan al-Karaji, qui vécut au tournant des Xe et XIe siècle. De certains de ses écrits, on peut déduire que ce mathématicien et ingénieur était encore en vie en 1015. Sinon, on sait peu de choses de la vie d'al-Karaji : il consacra la fin de son existence à l'étude de mécanismes hydrauliques et aurait produit la majeure partie de son œuvre mathématique lorsqu'il était en poste à Bagdad. Il est le premier à avoir libéré l'algèbre de la géométrie : ses travaux sur les polynômes ont ouvert la voie à leur manipulation formelle, certains prétendent même qu'il fut le premier à créer un véritable calcul algébrique. Traitant de polynômes, al-Karaji étudia également les coefficients binomiaux, qui le conduisirent à construire par induction le fameux « triangle de Pascal »… six siècles avant le philosophe français, mais quatre siècles après son homologue indien !
On retrouve également le fameux triangle dans les écrits d'Omar Khayyâm, qui développa dans la foulée la formule du binôme de Newton, six cents ans avant le savant britannique. Un nouvel exemple de fausse attribution… Dans son Traité sur les preuves des problèmes en algèbre, le poète et mathématicien écrit : « J'ai composé un livre afin d'expliquer la justesse des règles nécessaires pour obtenir la réponse des équations cubiques et pour extraire le côté du carré, du cube… Ces règles sont des nouveautés dans la science. Ces démonstrations sont arithmétiques. » À la fin de son existence, Khayyâm supervisera la construction d'un observatoire astronomique à Ispahan et contribuera à une réforme du calendrier solaire. Il proposera une mesure de la durée de l'année solaire correspondant à 365,2422 jours. Difficile de faire beaucoup mieux !
En Chine, en Allemagne, en Italie…
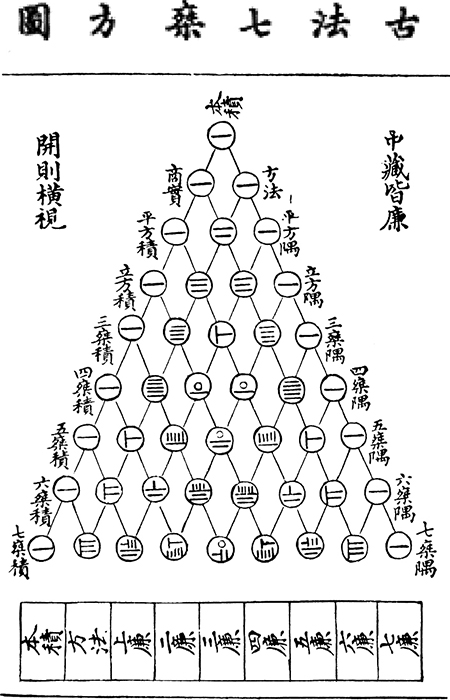
Le triangle fut également exporté en Chine. C'est Hui Yang qui nous l'apprend, dans son ouvrage Xiangjie Jiuzhang Suanfa (« Analyse détaillée de neufs chapitres de procédures mathématiques »). Yang y expose une méthode de recherche des racines carrées et cubiques utilisant le triangle tout en précisant : « Ma méthode pour extraire les racines carrée et cubique est basée sur la méthode de Jia Xian présentée dans le Shi Suo Suan Shu [« neufs chapitres de l'art mathématiques », un livre aujourd'hui perdu]. » Ce serait donc au mathématicien Jia Xian (vers 1010, vers 1070) que reviendrait le crédit de la construction du triangle en Extrême-Orient.
Et en Europe ? Son apparition est beaucoup plus tardive. On retrouve le triangle dans un ouvrage d'arithmétique commerciale (Ein newe und wolgegründete Underweisung aller Kauffmanns Rechnung in dreyen Büchern, mit schönen Regeln und fragstücken Begriffen) publié en 1527 et dû à la plume du mathématicien et astronome allemand Peter Bienewitz, mieux connu sous son pseudonyme de Petrus Apianus (1495–1552). Il latinisa son nom en observant que l'allemand Biene, signifiant « abeille », se traduisait en latin par apis. L'astronome publia aussi une table des sinus.
On retrouve également le triangle mal nommé dans les écrits du moine fanatique allemand Michael Stifel (vers 1486–1567).
Pascal : une approche moderne
En Italie, le triangle de Pascal est connu sous l'appellation triangolo di Tartaglia (« triangle de Tartaglia »), en hommage au mathématicien bègue du XVIe siècle. Alors ? D'où peut bien provenir cette attribution étonnante de « triangle de Pascal » ? C'est que le mathématicien philosophe français lui a consacré tout un traité en démontrant rigoureusement une somme de propriétés admises jusque-là sans preuves formelles. Rédigé en 1654 et publié un an plus tard, le Traité du triangle arithmétique reprend les résultats antérieurs de Tartaglia (publiés en 1556) et de Michael Stifel (datant de 1543) mais en en donnant une présentation théorique unifiée et rigoureuse et, surtout, en introduisant le raisonnement par récurrence. Ce sont dix-neuf lemmes et théorèmes qui sont démontrés tout au long du traité sous les appellations modestes de « conséquences ». Et Pascal de conclure, dans la plus pure tradition des mathématiciens de génie qui considèrent certains raisonnements comme triviaux et ne devant donc pas être explicités : « On peut tirer de là beaucoup d'autres propriétés que je supprime, parce que chacun les peut facilement conclure, et que ceux qui voudront s'y attacher en trouveront peut-être de plus belles que celles que je pourrais donner. »
Le traité est enfin complété par plusieurs applications. La première traite de l'Usage du triangle arithmétique pour les ordres numériques. Pascal introduit ce qu'il appelle les « nombres de premier ordre », à savoir les simples unités : 1, 1, 1, 1… Il nomme « nombres du second ordre » les naturels qui se forment par l'addition des unités : 1, 2, 3, 4… Les « nombres du troisième ordre » sont ceux qui se forment par l'addition des naturels : 1, 3, 6, 10… ; ce sont ceux qu'ils appelle « nombres triangulaires ». Pascal nomme ensuite « nombres du quatrième ordre » les sommes des précédents : 1, 4, 10, 20…, qu'il qualifie de « pyramidaux », pour arriver aux « nombres du cinquième ordre » ou « triangulo-triangulaires » : 1, 5, 15, 35… Il reconstruit ainsi le tableau initial du mathématicien indien Varāhamihira. La boucle est bouclée.
Mais Pascal entrevoit bien d'autres applications au triangle. Il termine son traité par l'Usage du triangle arithmétique pour les combinaisons, suivi de l'Usage du triangle arithmétique pour déterminer les partis qu'on doit faire entre deux joueurs qui jouent en plusieurs parties. Il conclut enfin par l'Usage du triangle arithmétique pour trouver les puissances des binômes et des apotomes, ce dernier terme désignant pour Pascal les résultats de différences entre un nombre quelconque A et un certain nombre entier donné. Le mathématicien établit en fait les formules bien connues aujourd'hui pour calculer (A – k)n avec k et n deux entiers.
Tous les résultats concernant le triangle arithmétique préexistaient. Ils étaient bien connus. Mais Pascal fit un vrai travail de mathématicien, au sens moderne, en présentant une théorie complète, rigoureuse et définitive, s'appropriant tous les résultats tout en nous en fournissant une version facilement accessible.