« “Voyez-moi ça ! dit le diable.[…] Continuons à assembler les cubes. La pierre suivante vient toujours se placer sur la jointure entre les deux qui sont en-dessous, comme font les maçons.” […] Et ils continuèrent jusqu'à ce que le triangle soit terminé. […] Le démon des maths grimpa le long d'un des côtés du triangle et écrivit un “1” sur le cube situé au sommet. […] “Sur chaque cube, nous écrivons toujours le résultat de l'addition des nombres placés au-dessus.

– Un jeu d'enfant”, dit Pierre. »

Comme Pierre, l'enfant en proie au « démon des maths » dans ses rêves, admirablement contés par Hans Magnus Enzensberger dans le titre éponyme (Le Seuil/Métaillé, 1998), nous irons de découverte en découverte au cœur du triangle de Pascal.

D'innombrables figures numériques

Le triangle suggéré par le démon des maths.

« “Ce triangle contient encore bien mieux” affirme le démon des maths à Pierre, déjà émerveillé par cet entassement triangulaire de cubes ne possédant pour propriété que celle de son algorithme de construction. Blaise Pascal avait, déjà, dans l'étude détaillée qu'il a faite de “son” triangle en 1653, décelé une multitude de propriétés découlant de cet empilement, révélant : “J'en laisse bien plus que je n'en donne. C'est une chose étrange combien il est fertile en propriétés, chacun peut s'y exercer.” »

Les premières propriétés qui sautent aux yeux sont celles de symétrie : le tableau est symétrique par rapport à son axe médian, celui que Pascal appelait « la dividente ». Cette propriété vient de la disposition des premiers « 1 » du triangle et le petit Pierre n'a pas manqué de le remarquer.

Bien avant le démon des maths, Pascal avait, dans son Traité du triangle arithmétique, consacré une mention spéciale aux « ordres numériques », c'est-à-dire aux « nombres figurés » qu'on peut lire dans ce triangle. On y voit successivement les nombres triangulaires – cases bleu turquoise – qui sont là parce qu'ils sont sommes des premiers entiers : 3 = 1 + 2, 6 = 1 + 2 + 3…, toujours à cause de l'algorithme de construction du triangle. Puis viennent les nombres que Pascal appelait « pyramidaux », et que nous nommons tétraédriques – cases roses –, sommes des premiers nombres triangulaires : 4 = 1 + 3, 10 = 1 + 3 + 6…, puis les nombres – cases jaunes – qu'il nomme « triangulo-triangulaires » car, dit-il, ils n'ont pas de nom. Il en va ainsi « jusqu'à l'infiny ». Mais ce n'est pas tout !

Le démon l'a fait remarquer au petit Pierre : la somme des nombres par ligne double à chaque fois, propriété immédiate, toujours à cause de l'algorithme de construction. La somme des nombres écrits en bleu, 28, est par exemple le double de la somme des nombres écrits en rouge, si bien que l'on peut démontrer par récurrence que la somme des nombres de la n^ème ligne est égale à 2ⁿ. Pascal n'avait pas, lui non plus, omis de le mettre en évidence. Dans sa longue liste de dix-neuf « conséquences », provenant précisément de la construction même du triangle, cette propriété figure à la septième place : « En tout triangle Arithmétique, la somme des cellules de chaque base est double de celles de la base précédente. »

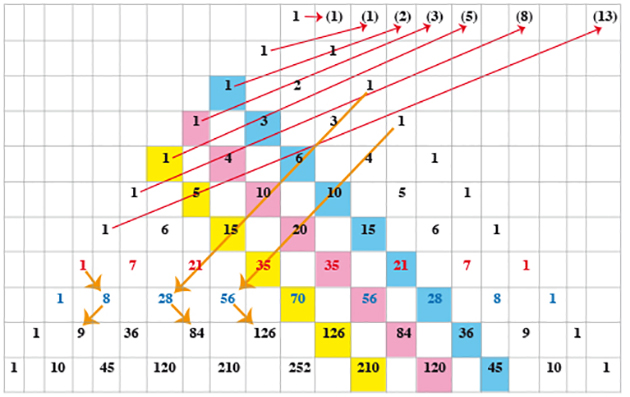
Mais voilà que, dans ce triangle, pour Pierre, s'invitent aussi « les nombres des lapins ». Vous l'aviez deviné, il s'agit des éléments de la suite de Fibonacci, celle dont les deux premiers termes sont 1 et 1, les suivants étant obtenus en additionnant chaque fois les deux termes précédents. Eh bien oui, la célèbre suite apparaît effectivement en sommant les diagonales ascendantes, ses termes successifs figurant entre parenthèses : 1, 1, 1 + 1 = 2, 1 + 2 = 3, 1 + 3 + 1 = 5, 1 + 4 + 3 = 8, 1 + 5 + 6 + 1 = 13… Le triangle de Pascal renferme donc de nombreux trésors numériques. Mais ce n'est toujours pas tout !

De remarquables figures géométriques

En plus de toutes ses particularités numériques, le triangle de Pascal cache aussi son lot de figures géométriques. Les plus simples sont en « crosse de hockey », comme les tracés couleur ocre. Additionnez les ombres le long de la canne, vous obtenez le résultat au bout de la « palette » et cela tient encore à l'algorithme de construction du triangle.

Voulez-vous une autre surprenante apparition de la géométrie dans le triangle de Pascal ? C'est cette fois le démon des maths qui nous met sur la voie. Ne conservons, dans le triangle, nous dit-il, que les nombres pairs, illuminons-les en orange, et cachons les autres.

   Le triangle de Sierpinski.

Cela ne vous rappelle rien, cette figure étrange qui apparaît ? Ne serait-ce pas un triangle de Sierpinski, ce fameux triangle équilatéral duquel on retire le triangle central, pour recommencer ainsi avec chaque nouveau triangle ?

Il en est de même en illuminant, au lieu des nombres pairs, tous les nombres multiples de n'importe quel entier p qui vous convient. Fractal, non ?

Nombres et suites remarquables dans le triangle de Pascal.

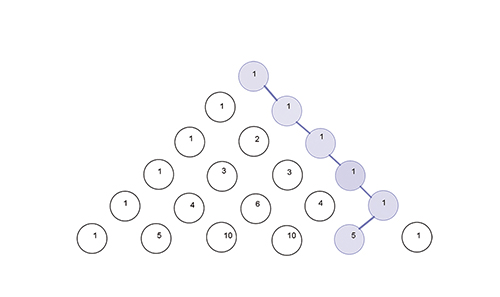
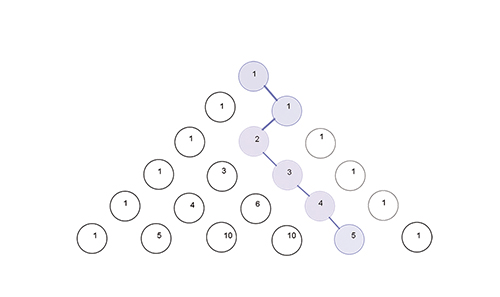
Une dernière particularité géométrique liée à la construction du triangle est la suivante : en considérant les nombres comme un réseau de points reliés entre eux selon les diagonales, chaque entier du triangle donne exactement le nombre de chemins possibles pour parvenir, sans retour en arrière, jusqu'à lui. En effet, pour parvenir à un nombre a, seuls deux chemins sont possibles : arriver par le haut, à droite depuis b ou à gauche depuis c. Le nombre de chemins pour arriver à a est donc égal à la somme des nombres de chemins pour arriver à b ou à c, ce qui n'est rien d'autre que la règle de construction du triangle.

Figure fractale dans le triangle de Pascal.

Les cinq chemins qui mènent au nombre 5

Une profusion de figures combinatoires  

Nous voici arrivés à l'usage le plus habituel de ce triangle, celui auquel Pascal avait consacré un chapitre, « Usage du triangle arithmétique pour les combinaisons ». Le mot, pour Pascal, avait besoin d'être expliqué : « Lorsque, de plusieurs choses, on donne le choix d'un certain nombre, toutes les manières d'en prendre autant qu'il est permis, entre toutes celles qui sont présentées, s'appellent les différentes combinaisons. » La définition reste très actuelle, seules les notations changent : nous écrivons aujourd'hui  \( \binom{n}{p}\) le nombre de façon de prendre p objets parmi n, et l'intérêt est que ces nombres interviennent dans le développement algébrique de (a + b)ⁿ. En effet, pour développer ce produit de n termes égaux à (a + b), nous aurons à prendre b dans p parenthèses et a dans les n – p restantes, pour obtenir le terme a ^n–p × b ^p, et il y a exactement \( \binom{n}{p}\)   façons de choisir les p parenthèses. On obtient donc en définitive :

\( (a+b)^n\)
\( = a^n \binom{n}{1}a^{n-1}b+\binom{n}{2}a^{n-2}b^2+...+\binom{n}{p}a^{n-p}b^p+...+b^n\)
\( =\sum\limits_{p=0}^{n}\binom{n}{p}a^{n-p}b^{p}.\)  

Voilà pourquoi on nomme coefficients binomiaux les nombres de combinaisons qui interviennent ici. Ces nombres possèdent la propriété remarquable de vérifier  

\( \binom{n}{p} = \binom{n-1}{p-1}+\binom{n-1}{p}\)

 puisque, sur toutes les combinaison de p objets pris parmi n, \( \binom{n-1}{p-1}\) contiennent un objet a fixé et \( \binom{n-1}{p}\)   ne le contiennent pas.

La boucle est bouclée : si on range les coefficients binomiaux par lignes selon les valeurs de n, ils vérifient la loi de construction du triangle arithmétique : ce sont exactement ceux de notre triangle !

À la lumière de cette identité combinatoire apparaissent d'autres propriétés, liées à la forme des coefficients binomiaux. Ils ont une forme très particulière : 

\( \binom{n}{p} = \frac{n!}{p!\times (n-p)!}\)

où p! désigne le nombre de permutations de p objets : on a en effet p façons de choisir le premier, p – 1 de choisir le deuxième, etc., si bien que :

p! = p × (p – 1) × (p – 2) ×… × 2 × 1,

soit le produit des p premiers entiers. Ainsi, 

\( \binom{n}{p} = \frac{n\times(n-1)\times ... \times (n-p+1)}{p\times (p-1)\times ...\times 2 \times 1}\)

Cette écriture va permettre de mettre en évidence une propriété supplémentaire du triangle de Pascal : sur toutes les lignes de ce triangle dont les numéros sont des nombres premiers, tous les nombres sauf les « 1 » des deux extrémités sont divisibles par le numéro de la ligne.

Soit donc la ligne numéro n, avec n premier, du triangle. Les entiers de cette ligne s'écrivent 

\( \binom{n}{p} = n \times \frac{N}{p!},\)

où N = (n – 1) × (n – 2) × … × 2 × 1 et p varie de 1 à n – 1, puisque l'on exclut les nombres extrêmes. Or les nombres du triangle sont entiers, donc p! va diviser n × N. Comme par ailleurs tous les facteurs de p! sont inférieurs à n, qui est premier, p! et n sont premiers entre eux ; c'est donc que p! divise N, et du coup le nombre \( \binom{n}{p}\)   est divisible par n.

« “Je n'aurais pas imaginé cela, même en rêve” dit Pierre. “Tu as raison, les mathématiques sont une histoire sans fin” dit le démon. “Tu creuses, tu creuses, et tu finis toujours par trouver encore du nouveau.” »