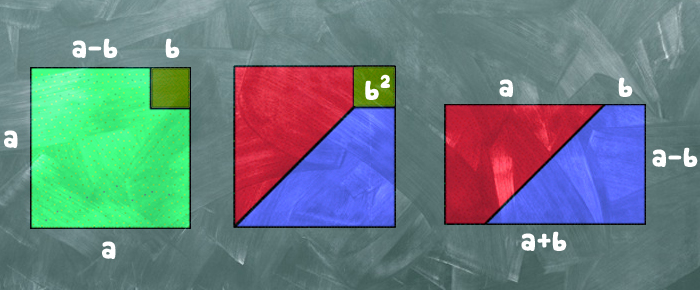
Les fameuses « identités remarquables » ont été, selon une longue tradition d'enseignement des mathématiques en France, l'un des piliers du calcul algébrique. Elles font partie – pas toujours explicitement d'ailleurs des savoirs transmis, enseignés et utilisés depuis qu'il existe des écoles mathématiques, mais si elles ont fait les beaux jours des programmes d'enseignement de l'algèbre au niveau du collège, elles n'apparaissent plus qu'en pointillés dans la version 2016 des programmes de troisième…
Toute une histoire…
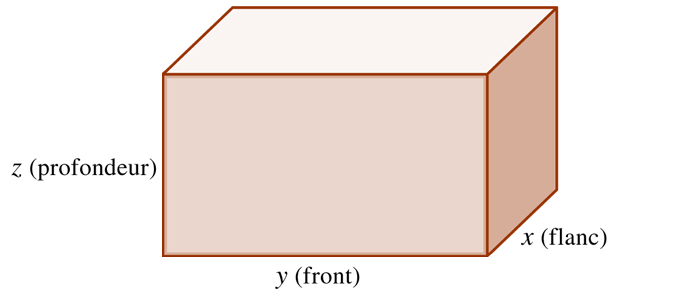Environ deux mille ans avant notre ère, les Babyloniens de l'Ancien Âge consignaient déjà sur leurs tablettes destinées à l'enseignement des scribes « porteurs de savoir » des problèmes avec solutions où intervenaient largement les identités remarquables. Ils recherchaient par exemple deux nombres connaissant leur somme et leur produit, dans un étonnant problème concret : « Une cave. Le flanc, le front [inverses l'un de l'autre], la profondeur, somme du flanc et du front. J'ai extrait 26 de terre. Que sont le flanc ? le front ? la profondeur ? » Nous dirions aujourd'hui : rechercher x (le flanc), y (le front), z (la profondeur) d'une cave sachant que xy = 1, x + y = z et xyz = 26.
En tenant compte du changement d'unités entre les dimensions horizontales (en nindas) et les dimensions verticales (en coudées, avec 1 ninda = 12 coudées), le scribe babylonien est amené à
que le traducteur a noté 2°10' puisque le système de numération est en hexagésimal, comme les mesures d'angles, ce qui donne
Hormis cette demi-somme, le calculateur va faire intervenir la demi-différence, tenant compte du fait – et c'est là qu'interviennent les identités remarquables que
Il en déduit
et
Ainsi, x et y seront déterminés grâce à leur demi-somme et à leur demi-différence, et x = 1°30', y = 40'.
Vers l'an 250 de notre ère, Diophante d'Alexandrie utilise, lui, couramment, dans son ouvrage célèbre les Arithmétiques, les développements du carré et du cube d'une somme de deux termes ou celui du produit de leur somme par leur différence.
L'ouvrage, loin d'être théorique, est un recueil, en treize livres dont dix seulement ont été retrouvés, les quatre derniers en 1972, de plus de cent quatre-vingts problèmes en grande partie résolus par équations. Vraisemblablement dédié à l'origine au « vénérable Dionysios », archevêque d'Alexandrie, il était destiné à l'enseignement. Voici l'un des premiers usages de ce qui deviendra par la suite les « identités remarquables », le problème XXVIII du Livre I :
« Trouver deux nombres tels que leur somme et la somme de leurs carrés forment des nombres donnés. »
Les identités remarquables sont présentes dès la première ligne : « Il faut toutefois que le double de la somme des carrés des nombres excède d'un carré le carré de la somme des nombres. » Rappelez-vous : si a et b sont les deux nombres cherchés, 2(a2 + b2) – (a + b)2 est effectivement égal à (a – b)2. Bonne remarque ! L'auteur propose ensuite que la somme des nombres soit de 20 unités et que la somme de leurs carrés forme 208 unités. Pour la résolution, Diophante utilise, comme à son habitude, une inconnue auxiliaire, qu'il appelle arithme et qui l'amène à poser, si a > b, a – b = 2t. Il va alors, comme les Babyloniens, exprimer chaque nombre en fonction de la demi-somme et de la demi-différence t de a et b :
Là interviennent à nouveau des identités remarquables : « La somme de leurs carrés, qui forme 208 unités, forme deux carrés d'arithme plus 200 unités. » En effet, a2 + b2 = 208 s'écrit bien (t + 10)2 + (t – 10)2 = 208, ou encore 2t2 + 200 = 208. C'est ainsi que « l'arithme devient deux unités » et que « le plus grand nombre sera 12 unités, le plus petit 8 unités, et ces nombres satisfont à la proposition ».
Une vraie mine !
Bien après Diophante, François Viète, l'un des plus grands mathématiciens de son temps, inventeur de l'écriture algébrique littérale, développe des applications essentielles de sa « nouvelle algèbre » dans ses Zététiques, dont la première publication date de 1591.
Sur cinq livres, il aborde, pour la formation de ses quelques élèves, qui poursuivront son œuvre, toutes sortes de problèmes de recherches de quantités connaissant leur somme ou leur différence, leur quotient ou leur produit ; une vraie mine d'identités remarquables !
La Zététique III du Livre I présente le problème suivant : « Étant donné le rectangle sous les côtés et la différence d'iceux, on trouvera les côtés. » La résolution commence par l'énoncé d'un théorème : « Le carré de la différence des côtés ajouté au quadruple du rectangle contenu sous iceux est égal au carré de la comme des côtés. » On l'exprimerait aujourd'hui simplement par (a – b)2 + 4ab = (a + b)2. Ici, on connaît le produit ab, la différence a – b, et Viète propose de calculer les deux côtés par l'intermédiaire de leur somme et de leur différence, donnant vers la fin une application pratique : « Soit le rectangle sous les côtés : 20, desquels la différence est : 8. » Ainsi, d'après le théorème précédent, le carré de la somme est 82 + 4 20 = 64 + 80 = 144, la somme des côtés vaut donc 12. Leur différence étant 8, les deux côtés seront 2 et 10. L'artifice de calcul est efficace.
Les manuels de mathématiques regorgent de problèmes relevant des identités remarquables, une tradition, presque une manie, qui s'est répandue dans l'enseignement, où l'étude du trinôme du second degré et sa mise sous forme canonique ont fait les beaux jours de l'enseignement des mathématiques dans le secondaire. Les identités remarquables à proprement parler, qui figurent dans le programme de seconde en 1947, puis dans celui de troisième en 1962, prennent place dans les programmes de 1985, en quatrième sous la forme « développement d'expressions du style (a + b)(c + d) », puis en troisième, avec « factorisation d'expressions de la forme a2 – b2, a2 + 2ab + b2, a2 – 2ab + b2 ». Les manuels scolaires ne demandent pas tant de retenir ces identités, même si certains exigent qu'elles soient « sues par cœur », que de les appliquer, encore et encore. On trouve en plus des classiques, carré de la somme de deux termes, carré de leur différence, produit de la somme de deux nombres par leur différence, des identités plus exotiques. Le célèbre manuel « Lebossé–Hémery » de 1951 pour la classe de troisième présente (a + b + c)2, (a + b)3, (a - b)3, (a + b)(a2 – ab + b2), (a - b)(a2 + ab + b2), (a + b)2 + (a – b)2 et enfin (a + b)2 – (a – b)2, précisant « qu'elles pourront être vérifiées à titre d'exercices ».
Un lien avec le calcul mental
À quoi bon tant d'identités remarquables dans l'enseignement secondaire ? Les manuels ne les présentent jamais comme une fin en soi, mais la plupart d'entre eux exploitent surtout le lien avec le calcul mental. On calcule ainsi plus aisément le carré d'un nombre terminé par 1 ou par 9, celui d'un nombre terminé par 5 vient aisément. Ces fameuses identités se révèlent aussi utiles pour calculer mentalement des produits comme 32 28, 28 22 ou 57 43. Dans les nombreux exercices qui sont proposés sur la question, on voit revenir le thème dans des vérifications d'identités comme : (a + b + c)2 – 3(a + b)(b + c)(c + a) = a2 + b2 + c2 ou dans les procédés de factorisation de certains polynômes. On en fait également une utilisation timide en géométrie (voir en encadré).
Dans les programmes 2008 de collège, les identités remarquables font toujours partie des « connaissances ». Si elles sont exigibles pour le socle commun, il est précisé « qu'aucune mémorisation des formules n'est exigée ». Dans les programmes 2016, les identités ont changé de statut, puisqu'elles ne font désormais plus partie des « connaissances et compétences associées » du cycle 4 d'enseignement secondaire, mais sont juste données à titre « d'exemples de situations d'activités et de ressources ». Elles figurent désormais sous le seul label « étudier les problèmes qui se ramènent au second degré (par exemple, en factorisant des équations produits simples à l'aide d'identités remarquables ». Leur disparition au prochain numéro ?