Le développement du binôme

On a coutume de nommer l'expression (1 + x)ⁿ binôme de Newton, même si elle était utilisée bien avant la naissance de Newton, en particulier par les mathématiciens perses dès le x^e siècle, de même que le « triangle de Pascal » qui lui est associé. La formule du binôme concerne le développement de (1 + x)ⁿ comme somme de multiples des polynômes 1, x, x², x³, etc.

Pour n = 2 et n = 3, on trouve les identités remarquables (1 + x)² = 1 + 2x + x² et (1 + x)³ = 1 + 3x + 3x² + x³.

On passe à la puissance 4 en remarquant que (1 + x)⁴ = (1 + x)(1 + 3x + 3x² + x³).

En généralisant ceci, on obtient le tableau ci-dessous, où les développements des binômes de la colonne de gauche se lisent sur la ligne correspondante. Ainsi en quatrième ligne, on lit (1 + x)⁴ = 1 + 4x + 6x² + 4x³ + x⁴.

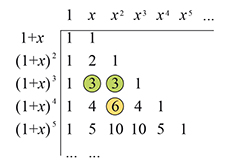Triangle de Pascal et formule du binôme de Newton. Le terme entouré en jaune est égal à la somme des termes entourés en verts.

Le coefficient de x^k dans le développement de (1 + x)ⁿ est appelé la combinaison de k parmi n, et noté \( C^k_n\) ou 

\( \dbinom{n}{k}.\)

La formule du binôme s'écrit alors 

\( (1+x)^n=\sum\limits_{k=0}^n\dbinom{n}{k}x^k.\)

Elle se démontre facilement par récurrence sur n.

Ces coefficients vérifient diverses formules de récurrence, comme celle qui ressort de la construction du triangle de Pascal :

\( \dbinom{n}{k}+\dbinom{n}{k+1}=\dbinom{n+1}{k+1}.\)
 

On peut également exprimer les combinaisons en fonction de factorielles : 

\( \dbinom{n}{k}=\frac{n!}{k!(n-k)!}.\)

Enfin, en remplaçant x par le quotient x / y, la formule du binôme se généralise facilement à 

\( (x+y)^n=\sum\limits_{k=0}^n \dbinom{n}{k}x^ky^{n-k}.\)

Loi binomiale

En probabilités, la loi binomiale exprime que la probabilité de k succès dans une série de n expériences, dont la probabilité de chacune est égale à p, est égale à 

\( \dbinom{n}{k}p^k(1-p)^{n-k}.\)
 

  Cette loi possède de nombreuses applications, en particulier pour justifier la qualité des sondages probabilistes (voir Tangente 140) ou étudier la probabilité de faillite d'une compagnie d'assurance-accident (voir les Mathématiques des assurances, Bibliothèque Tangente 57). Inversement, on peut en déduire une démonstration de la formule du binôme puisque la somme des probabilités ci-dessus est égale à 1, d'où, sans calcul,  si 0 < p < 1

\( \sum\limits_{k=0}^n \dbinom{n}{k}p^k(1-p)^{n-k}.\)

Si l'on considère deux nombres x et y strictement positifs, en posant \( p=\frac{x}{x+y} \) , on obtient  \( 1-p=\frac{x}{x+y} \) et on en déduit la formule du binôme. On peut conclure en considérant le polynôme différence, qui ne peut avoir une infinité de zéros sans être nul. 

Des formules qui découlent du binôme 

Plusieurs formules intéressantes peuvent être déduites de celle du binôme. Par exemple, en substituant 1 ou –1 à x, on obtient 

\( \sum\limits_{k=0}^n \dbinom{n}{k}=2^k\)

  et

\( \sum\limits_{k=0}^n \dbinom{n}{k}(-1)^k=0\)

En utilisant les formules d'Euler liant les fonctions trigonométriques et les exponentielles complexes, telle que 

\( \cos{x}=\frac{e^{ix}+e^{-ix}}{2}\)

  on peut calculer les puissances de cos x. Par exemple, la puissance quatrième donne 

\( \left(\cos{x}=\frac{e^{ix}+e^{-ix}}{2}\right)^4\)

  puis 

\( \frac{e^{4ix}+4e^{2ix}+6+4e^{-2ix}+e^{-4ix}}{16},\)

  et donc, en regroupant : 

\( \cos^4x=\frac{\cos 4x+3\cos 2x+3}{8}.\)

 On peut ainsi exprimer toute puissance de cosinus (ou de sinus) en fonction d'une somme de cosinus et de sinus.

Une formule analogue à la formule du binôme gouverne le calcul des dérivées successives du produit de deux fonctions. Plus précisément, si f et g sont deux fonctions n fois dérivables, le produit f × g l'est aussi, et 

\( (f\times g)^{(n)}=\sum\limits_{k=0}^n \dbinom{n}{k}f^{(k)}\times g^{(n-k)}\)

  où f (n) désigne la dérivée d'ordre n de f et f ⁽⁰⁾ = f. La démonstration se calque sur celle de la formule du binôme.