Le passe-dix
Vous connaissez le jeu de passe-dix ? On lance trois dés. Si la somme indiquée par les faces supérieures des trois dés dépasse dix, alors le lanceur est gagnant, sinon il perd. Le jeu est ancien et a suscité de nombreux problèmes. L'écrivain français du XIXe siècle Villiers de L'Isle-Adam regrettait que « les cornets de passe-dix roulaient des dés sur des enjeux capables d'affamer des provinces ».
Quelle est la probabilité de gain du lanceur ? On peut effectuer de longs calculs combinatoires pour évaluer la probabilité de chaque tirage, mais il est plus astucieux de remarquer que la somme des chiffres sur deux faces opposées d'un dé est égale à 7. Le total pour les trois dés des chiffres inscrits sur les faces opposées d'un dé est donc égale à 21.
À chaque tirage de trois dés dont la somme est inférieure à 10 correspond, sur les faces symétriques (bases sur lesquelles les dés reposent), une somme supérieure à 10… et inversement. Donc la probabilité de gain est 1/2. Tout simplement !
Le duc de Toscane s'était étonné que la somme 10 apparaisse plus souvent que la somme 9, alors qu'elles ont toutes deux six façons d'apparaître (10 = 6 + 3 + 1 = 6 + 2 + 2 = 5 + 4 + 1 = 5 + 3 + 2 = 4 + 4 + 2 = 4 + 3 + 3, et 9 = 6 + 2 + 1 = 5 + 3 + 1 = 5 + 2 + 2 = 4 + 4 + 1 = 4 + 3 + 2 = 3 + 3 + 3). Galilée résout le problème en calculant que 9 peut apparaître de vingt-cinq manières différentes, alors que 10 apparaît de vingt-sept manières différentes, parmi les deux cent seize combinaisons possibles. Il est donc plus facile d'obtenir 10 que 9.
La corde du cercle : attention danger !
Les paris fondés sur des raisonnements géométriques ne sont pas sans danger d'erreur. Quelle est la valeur de la « corde moyenne » d'un cercle ? Selon que vous prenez les cordes issues d'un point sur la circonférence, parallèles à une direction donnée, ou d'orientation aléatoire, vous trouverez des valeurs différentes.
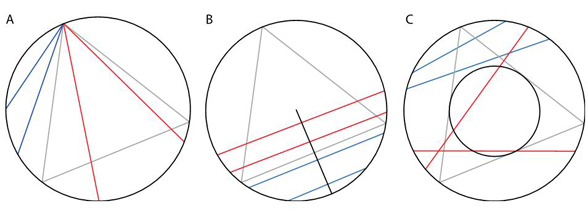
La probabilité que la corde soit plus grande que le coté du triangle équilatéral inscrit dans le cercle (figure A) est de 2/3. Elle vaut 1/2 si les cordes sont parallèles, et donc centrées sur un diamètre (figure B). Elle égale au quotient de l'aire du cercle de rayon 1/2 par l'aire du grand cercle, soit 1/4, si l'on choisit le centre et que l'on prend une orientation arbitraire (figure C).
Ainsi, la réponse dépend de la façon dont l'expérimentateur décrit le monde en modélisant la situation. C'est le paradoxe de Bertrand, qui a été résolu par un examen approfondi du mot « corde aléatoire », mais cela est une autre histoire…
L'aiguille de Buffon
Le premier problème de probabilité géométrique est peut-être celui de l'aiguille de Buffon. Il s'agit de déterminer la probabilité qu'une aiguille de longueur L jetée sur un parquet (que l'on suppose infini), dont les lames parallèles sont espacées d'une largeur D, coupe une droite entre deux lames. Pour calculer cette probabilité, on peut « bourriner », à grands coups de calcul intégral, ou… réfléchir, comme l'a fait le mathématicien Émile Borel.
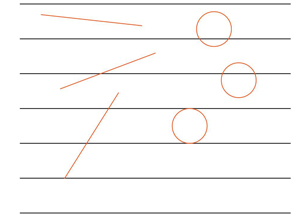Désignons par P la probabilité que l'aiguille coupe une droite : P est proportionnelle à la longueur L de l'indispensable outil de la couturière. La probabilité P est de même inversement proportionnelle à la largeur D, donc P = k L/D pour une certaine constante k > 0 à déterminer. Comme Borel, supposons que la forme de l'aiguille importe peu (l'hypothèse est osée, mais justifiée par le résultat final !). Pour une aiguille en forme de cercle de diamètre égal à l'espacement D des lames, le nombre d'intersections est toujours égal à 2. Comme le périmètre du cercle est
Georges-Louis Leclerc, comte de Buffon (1707–1788), affirma qu'il avait déterminé par cette méthode la valeur de