C'est, jusqu'au dernier quart du XIX^e siècle, l'économie politique qui a prévalu, mais l'économie mathématique s'est introduite, et durablement, apportant à la « science économique » la force d'un raisonnement qui lui faisait défaut. L'histoire de cette transformation est jalonnée de la pensée et des travaux de divers chercheurs, tant européens qu'américains. Parmi eux, un mathématicien français, Antoine-Augustin Cournot, a introduit de nombreux concepts nouveaux, repris et largement utilisés jusqu'à aujourd'hui.
 

L'arithmétique politique

En économie, il y a un « avant » et un « après » Cournot. « Avant » remonte à loin, puisque l'un des plus anciens traités abordant le sujet est celui de Xénophon (–430 ; –355), philosophe et militaire de la Grèce antique, élève de Socrate. On voit dans son ouvrage Οἰκονομικός, « L'Économique », apparaître le mot, fait de οἶκος, « maison » et de νόμος, « loi ». Il y traite, sous forme d'un dialogue socratique, de « l'art et la manière de bien gérer un grand domaine agricole ». Les arguments de ce dialogue, entre Socrate et Critobule, riche propriétaire terrien, sont plutôt philosophiques, Socrate prouvant à son interlocuteur qu'il est « pauvre dans sa richesse, et que lui, Socrate, est riche dans sa pauvreté ». Une seule théorie à retenir – elle figure dans le dernier chapitre – : « En agriculture comme en politique, en économie, à la tête des armées, le point essentiellement utile est le talent de commander. » Très peu de théorisation de l'économie, donc, et de raisonnement mathématique point puisque, pour Xénophon comme pour Socrate, il ne faut connaître de mathématiques que ce qui est utile. Leur place est donc celle d'être réduites à un outil.

Plus tard, à la Renaissance, puis à partir du XVII^e siècle, l'économie échappe à l'emprise de la morale puis de la politique pour devenir une science sociale autonome. Rares sont cependant les auteurs qui traitent du sujet en y introduisant des mathématiques. Déjà novateur, le Britannique William Petty (1623–1687), esprit universel, non seulement jette les bases de la démographie statistique, mais introduit une pratique scientifique dans la comptabilité nationale, dans les principes de la taxation et de la dépense publique, lie par des fonctions production de richesse, offre de monnaie et vitesse de circulation de celle-ci. « L'arithmétique politique », comme il l'appelait, était née. À sa suite, le Français Pierre Le Pesant de Boisguilbert (1646–1714) ou l'Irlandais Richard Cantillon (1680–1734) vont, pour le premier, créer un modèle expliquant la circulation de l'argent dans la société et, pour le second, lier le niveau des prix ainsi que le taux d'intérêt à l'offre et à la demande, toutes considérations déjà mathématiques.

En plein XVIII^e siècle, un mathématicien, cette fois, le Suisse Daniel Bernoulli (1700–1782), travaille les données économiques avec des séries et des équations différentielles, il reprend et explique dans un mémoire de 1738, Exposé d'une nouvelle théorie du risque, le paradoxe de Saint-Pétersbourg, proposé initialement par son cousin Nicolas (voir Théorie des jeux, Bibliothèque Tangente 46). Ainsi, vous préférez miser 1€ pour avoir une chance sur deux d'en gagner 2 plutôt que miser 50 € pour avoir une chance sur deux d'en gagner 100. Ce fait remet en cause la notion d'espérance de gain. Nicolas Bernoulli la remplacera par un critère d'utilité : « La détermination de la valeur d'un objet ne doit pas être basée sur ses avantages mais seulement sur l'utilité qu'il procure. » Autres précurseurs de l'économie mathématique, le Français Nicolas-François Canard (vers 1750–1833), professeur de mathématiques spéciales devenu économiste, développe ses thèses économiques sous un jour mathématique dans ses Principes d'économie politique (1801), le Britannique Thomas Perronet Thompson (1783–1869), homme politique et mathématicien, applique le calcul différentiel à la détermination du profit maximum, et l'Allemand Johann Heinrich von Thünen (1783–1850) utilise le calcul infinitésimal dans ses écrits comme L'État isolé en lien avec l'agriculture et l'économie nationale.

Pionnier dans tous les domaines 

Né à Gray, en Haute-Saône, Antoine-Augustin Cournot a indiscutablement une formation mathématique : il prépare le concours d'entrée à l'École normale supérieure, qui ferme en 1822 pour raisons politiques, avant qu'il ait pu y achever sa scolarité, mais, licencié en droit en 1827, devient docteur ès sciences (spécialité mathématiques) en 1829. Il fréquente déjà assidument le salon de l'économiste Joseph Droz, mais reste dans les mathématiques en tant que professeur d'analyse et mécanique à la faculté des sciences de Lyon, puis président du jury d'agrégation de mathématiques. C'est en 1838 qu'il publie son premier traité liant mathématiques et économie, Recherches sur les principes mathématiques de la théorie des richesses. D'autres suivront, mais beaucoup plus tard, laissant à Cournot le temps d'occuper d'autres fonctions : en 1863, Principes de la théorie des richesses et en 1877, Revue sommaire des doctrines économiques. C'est dans le premier que Cournot permet de voir sous un jour nouveau l'introduction des mathématiques dans les études économiques, un concept nouveau pour son époque.

Soulignant, dans l'introduction à son ouvrage de 1838, que pour ses prédécesseurs en « économie politique », les mathématiques leur étaient « à peu près étrangères », il égratigne au passage l'ouvrage de Nicolas Canard et ceux d'autres auteurs, « esprits à qui les sciences mathématiques étaient à peu près étrangères ». Cournot déclare d'emblée son « intention d'y appliquer les formes et les symboles de l'analyse mathématique » tout en étant conscient qu'il est « sans doute difficile aujourd'hui de vaincre un préjugé que les bons esprits tels que Smith [l'économiste Adam Smith (1723–1790) est considéré comme le père de l'économie politique] et d'autres écrivains plus modernes ont contribué à affermir ». Il ira donc dans cette publication au-delà des signes   « l'analyse mathématique n'a pas seulement pour objet de calculer des nombres »  et ne se limitera pas à des considérations algébriques : il établira dans cet essai que « la solution des questions générales auxquelles donne lieu la théorie des richesses dépend essentiellement non pas de l'algèbre élémentaire mais de cette branche de l'analyse qui a pour objet les fonctions arbitraires ». Son ambition se limitera toutefois aux « premières notions de calcul différentiel et intégral », qui « suffisent pour l'intelligence de ce petit traité ». Il est déjà, dans cet usage des mathématiques, un pionnier.

Pionnier, Cournot l'est aussi dans les concepts qu'il introduit. L'un de ses grands succès a été d'avoir fourni, pour la première fois, une théorie complète des formes de marché, allant du monopole (un seul producteur vendant sa production sans concurrence) jusqu'à la concurrence « indéfinie » (les offreurs sont en foule) en passant par le duopole (juste deux offreurs) ou l'oligopole (quelques vendeurs se font concurrence face à un grand nombre
de demandeurs). Pour analyser une situation de duopole, il met en scène, très concrètement, deux propriétaires de deux sources dont les eaux alimentent le marché et il définit le « point d'équilibre » (dit point de Cournot) où chacun maximise son gain, préfigurant l'équilibre de Nash.

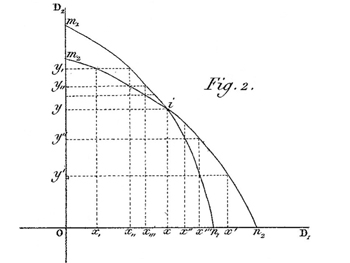
L'équilibre de Cournot en un graphique.

Cournot s'est également montré novateur en introduisant non seulement la « loi du débit » (loi de la demande) et en définissant la demande D comme une fonction du prix p. Écrire D = F(p) va lui permettre de rechercher la valeur de p qui rend maximum la valeur totale pF(p) de quantité « débitée » en résolvant l'équation F(p) + pF'(p) = 0. Illustrant la situation par un autre graphique, il décrira la racine de cette équation comme l'abscisse du point n pour lequel le triangle ont formé par la tangente (nt) et le rayon-vecteur on est isocèle, de sorte que oq = qt. 
 

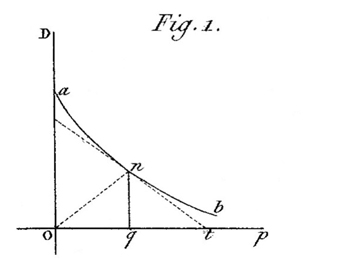
Le profit maximum selon Cournot.

Que de nouveaux concepts en devenir dans les écrits de Cournot ! Mais les fulgurances si pertinentes des Recherches ne seront vraiment reconnues que beaucoup plus tard. L'intéressé lui-même n'en a d'ailleurs guère assuré la promotion, abandonnant ce domaine pendant plusieurs années et n'y revenant que plus tard en publiant deux autres ouvrages consacrés à l'économie. Jules Dupuit (1804–1866) a d'ailleurs déjà rejoint Cournot sur ce terrain en publiant De l'utilité et de sa mesure en 1853, qui contient une quantité non négligeable de mathématiques. D'autres vont suivre : Léon Walras (1834–1910), qui publie en 1883 Théorie mathématique de la richesse sociale, William Stanley Jevons (1835–1882), dont The Theory of Political Economy a eu un grand succès, et Carl Menger (1840–1921), qui revendique de l'économie une approche scientifique dans ses Principles of Economics (1871). Sur cette lancée, on se met ensuite à appliquer à l'économie des principes de théorie des jeux développés par John von Neumann en 1928 et que John Nash a généralisés en 1950.

Les idées de Cournot ont peut-être mis du temps, mais elles ont fait leur chemin. L'intéressé écrivait justement à la fin de ses Souvenirs en 1859 : « Ceci est comme une bouteille que l'on met à part, dans l'idée qu'il viendra peut-être un jour où quelqu'un, s'avisant de l'ouvrir, en flairera volontiers le bouquet séculaire ; car il y a des choses qui, n'ayant d'abord que peu ou point de valeur, en gagnent avec le temps. »