La surface terrestre S d'une région peut être perçue comme étant la représentation graphique d'une fonction \( f\)  de deux variables x et y définie comme suit : \( f (x, y)\)  représente l'altitude de la projection orthogonale \( (x , y)\) , sur le plan horizontal situé au niveau de la mer, du point \( (x, y, f(x, y))\)  appartenant à S. On peut donner une image fidèle de S sur une feuille de papier en adoptant une technique bien connue en cartographie à propos des surfaces topographiques. Il suffit de représenter, sur une carte géographique de la région étudiée, quelques lignes de niveau : ce sont les projections dans le plan \( (xOy)\) des courbes de niveau qui sont l'intersection de S avec des plans horizontaux. La différence d'altitude entre deux plans horizontaux successifs est souvent choisie constante.

Où se trouve le mont Blanc ?

Gambadons dans une zone montagneuse comprenant un seul pic, comme autour du mont Cervin. Dans pareille situation, les lignes de niveau sont des courbes fermées emboîtées, leur cote étant d'autant plus grande que leur longueur est petite. Plus les lignes de niveau sont proches les unes des autres, plus la pente de la montagne est raide. Le point culminant du pic correspond au « centre » des lignes de niveau.

Arpentons à présent une zone montagneuse plus vaste, comprenant plusieurs pics, comme le mont Blanc. Tous les sommets répertoriés constituent des maxima locaux, c'est-à-dire des maxima dans de petits voisinages des points repérés. Pour trouver le maximum global, le point le plus haut d'un pays, on peut fixer son attention sur tous les maxima locaux repérés dans cette zone et choisir le pic le plus élevé. Hélas, ce raisonnement simple ne donne aucune assurance en ce qui concerne le « vrai » point culminant de la région !

Ce point est délicat. Examinons ainsi la question suivante : où est situé le point culminant de la chaîne des Alpes ? Certes, le mont Blanc est le plus haut sommet d'Europe occidentale, avec une altitude de 4 810 m (environ). Mais cet endroit est situé tantôt en France, tantôt en Italie, les deux pays n'étant pas d'accord sur le tracé de leur frontière commune.

À gauche : point de vue français (carte du capitaine Mieulet, 1865),
  À droite : Point de vue italien (atlas sarde, 1869).

Sur les cartes françaises, le mont Blanc est situé à l'intérieur d'une zone triangulaire approximative que la frontière franco-italienne contourne par le sud en se dirigeant vers l'est. Cette frontière repart ensuite brusquement en direction du nord, à peu près au niveau du mont Blanc de Courmayeur, dont le sommet, situé toujours en France, pointe à 4 748 m d'altitude : le point culminant de l'Italie se trouve à moins de cent mètres à l'est, à une altitude de 4 745 m.

Pour certaines versions italiennes, le sommet du mont Blanc de Courmayeur se trouve en Italie et la frontière entre les deux pays passe par le « vrai » mont Blanc. Ce différend géographique illustre bien le dilemme que l'on peut rencontrer en cherchant le maximum d'une fonction \( f\)  (l'altitude) sur un ensemble E (la France, l'Italie, ou la réunion des deux pays) : un éventuel maximum de \( f\)  sur E peut être atteint soit en un point intérieur à E (maximum local), soit en un point frontière de E.

Sentier de randonnée

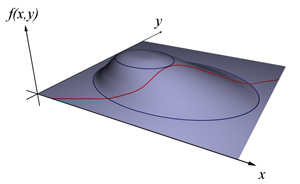Lors d'une randonnée sur un chemin de montagne, comment savoir que l'on atteint le point d'altitude maximale ? Déjà, un point où le chemin monte ou descend n'est certainement pas le plus haut. Or, le sentier où se trouve un tel point croise, par définition, une courbe de niveau. Aussi, le maximum d'altitude ne peut pas être atteint en un point où le sentier coupe une courbe de niveau. En langage mathématique, il s'agit de rechercher le maximum d'une fonction \( f\)  (l'altitude) sous une contrainte (déterminée par le sentier). Géométriquement, on souhaite donc trouver le point le plus haut parmi ceux de la surface S (la surface terrestre) représentative de \( f\)  qui appartiennent à la courbe (le sentier) décrite par la contrainte. Cette situation est illustrée par la figure suivante : la surface est dessinée en bleu, la contrainte définissant la courbe est tracée en rouge.

Si l'on projette la surface S sur le plan horizontal de base \( (xOy)\) , la contrainte définit une courbe (toujours en rouge sur la figure suivante), tandis que différentes lignes de niveau (en bleu) permettent de se faire une idée des valeurs prises par  \( f\)  (en fait, par l'altitude au-dessus des points du plan). Au point cherché, la ligne de niveau correspondante est tangente à la courbe définie par la contrainte : 

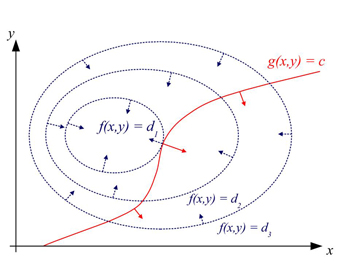
Cette règle est à la base de la méthode de Lagrange pour obtenir le maximum d'une fonction de deux variables sous une contrainte. Cette théorie peut être étendue, moyennant quelques aménagements d'ordre technique, aux cas d'objectifs comprenant plus de deux variables soumises à plus d'une contrainte.

Pour trouver le maximum d'une fonction \( f\)  de deux variables x et y, sous une contrainte du type g(x, y) = c, on construit d'abord le lagrangien L : on « retouche » l'objectif en ajoutant à \( f\)  un terme défini par la contrainte. Plus précisément, ce lagrangien dépend de trois variables (x, y et  \( \lambda\) ) et est défini par \( L(x, y, \lambda) = f(x, y) + \lambda[c-g(x, y)]\)  . Le coefficient \( \lambda\)  est appelé multiplicateur de Lagrange.

Ensuite, un point candidat à fournir un maximum de f sous la contrainte peut être trouvé en résolvant le système suivant en les trois variables retenues :

  \( \left( \dfrac{\partial\text{L}}{\partial x}=0~;~\dfrac{\partial\text{L}}{\partial y}=0~;~\dfrac{\partial\text{L}}{\partial \lambda}=0\right).\)

Les deux premières de ces équations traduisent géométriquement le fait que la courbe de niveau et la contrainte doivent être tangentes l'une à l'autre au point cherché (d'un point de vue vectoriel, le gradient de f est proportionnel au gradient de g en ce point). La troisième égalité du système redonne la contrainte.

Ainsi reformulé, le problème devient vulnérable à la puissance de l'analyse…