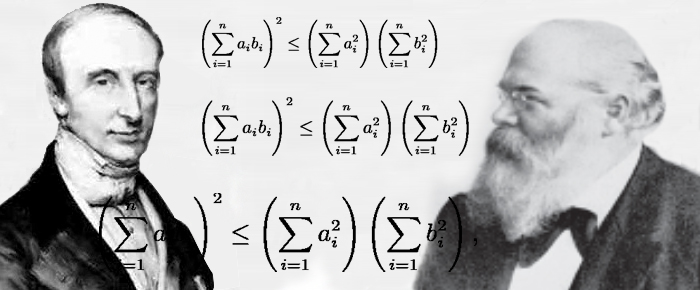
Le carré d'un nombre réel est toujours positif, et n'est nul que si le nombre lui-même est nul. Quoi de plus anodin ? Si l'on ajoute à ce résultat trivial l'identité remarquable donnant le carré d'une somme, c'est-à-dire (a + b)² = a² + 2 ab + b², on peut déjà traiter un bon nombre de questions d'optimisation. Donnons l'idée de base sur l'exemple de la maximisation du produit de deux nombres quand leur somme est donnée. Pour traiter cette question, notons 2a la somme donnée, x et y les deux nombres. Ils vérifient x + y = 2a, ce qui permet d'écrire y en fonction de x, et donc le produit xy sous la forme 2ax – x². L'identité remarquable rappelée ci-dessus invite à introduire le carré (x – a)². On obtient xy = a² – (x – a)². Comme le carré (x – a)² est toujours positif, et nul seulement si x = a, on en déduit que le maximum de xy est égal à a² et qu'il n'est atteint que si x et y sont égaux.

La même idée fonctionne pour trouver le minimum de la somme de deux nombres positifs quand leur produit est donné. Pour cela, il suffit d'écrire le produit et les deux nombres comme des carrés (de nombres positifs) : a², x² et y². L'égalité x²y² = a² implique xy = a. En utilisant l'identité remarquable, la somme des deux nombres s'écrit x² + y² = (x – y)² + 2xy, soit x² + y² = (x – y)² + 2a. Le minimum de la somme est donc égal à 2a, et il n'est atteint que si x et y sont égaux.

Ce résultat permet de trouver le minimum sur ]0, +∞[ de la fonction f définie par : 

  \( f(x)=x+\dfrac{{a}^{2}}{x}.\)

 
En effet, f (x) est alors égal à la somme x + y, où xy = a² si l'on pose :

  \( y=\dfrac{{a}^{2}}{x}.\)  

Le minimum est donc égal à 2a (si a > 0), ce que l'on peut retrouver sans problème par le calcul des variations de  f. En effet, l'étude du signe de la dérivée d'une fonction permet de déterminer ses variations, et donc ses extrema. Dans le cas de la fonction f , la dérivée est égale à :

  \( f'(x)=1-\dfrac{{a}^{2}}{{x}^{2}}=\dfrac{{x}^{2}-{a}^{2}}{{x}^{2}},\)  

qui est négatif sur ]0, a] et positif ensuite. La fonction décroît de 0 à a puis croît ensuite. Elle admet donc un minimum en a, ce minimum vaut f (a) = 2a.

 
L'inégalité arithmético-géométrique

De la même manière, la méthode permet de démontrer l'inégalité entre la moyenne arithmétique  \( \dfrac{a+b}{2}\) et la moyenne géométrique  \( \sqrt {{ab} }\)   de deux nombres positifs a et b. Pour cela, il suffit de les écrire sous forme de carrés ; on obtient 

\( \dfrac{a+b}{2}\ge\sqrt {{ab} }\) \( ≤\)

avec égalité si, et seulement si, a et b sont égaux. Par récurrence, cette inégalité se généralise aux moyennes arithmétiques et géométriques d'un nombre quelconque de nombres positifs a₁, a₂… a_n : on obtient 

\( $$\dfrac{a_1+a_2+...+a_n}{n}\ge\sqrt[n] {{a_1a_2...a_n} }$$\\\)  

avec égalité si, et seulement si, tous les a_i sont égaux. Augustin Cauchy (1789–1857) en a donné une démonstration merveilleuse (voir en encadré).

L'inégalité arithmético-géométrique permet de trouver des maxima quand des sommes ou des produits de termes sont constants. Deux exemples vont nous permettre d'expliciter ce point.

Déterminons le minimum sur ]0, +∞[² de la fonction g définie par

  \( g(x,y)=2x+4y+\dfrac{1}{xy}.\)

En appliquant l'inégalité aux trois nombres 2x, 4y et  \( \dfrac{1}{xy}\) , on obtient  \( \dfrac{g(x,y)}{3}\ge\sqrt[3] {8}\) avec égalité si, et seulement si,  \( 2x=4y=\dfrac{1}{xy},\)   

ce qui se produit si, et seulement si, x = 1 et y = 1 / 2. 

Le minimum de g est donc égal à 6, il est atteint pour x = 1 et y = 1 / 2.

De même, déterminons le maximum sur ]0, +∞[² de la fonction h définie par h(x,y) = xy (3-x-y).
On peut supposer 3–x–y ≥ 0 puisque sinon h < 0 ne correspond pas à un maximum.

En appliquant l'inégalité aux trois nombres positifs x, y et 3–x–y, on arrive à  \( \sqrt[3] {h(x,y)}\le1\)  avec égalité si, et seulement si, x = y = 3–x–y, c'est-à-dire si x = y = 1. Le maximum de h est donc 1 et il est atteint en x = y = 1.

L'inégalité de Cauchy–Schwarz

Une autre inégalité célèbre, souvent présentée dans un cadre géométrique, est due à Cauchy mais porte également le nom de Hermann Schwarz (1843–1921), qui l'a étendue à un cadre bien plus général. Si a₁, a₂… a_n et b₁, b₂… b_n sont des nombres réels, alors : 

(a₁b₁ + a₂b₂ + … + a_nb_n)² ≤ (a₁² + a₂²+ … + a_n²)(b₁² + b₂² + … + b_n²).

Le cas d'égalité correspond au cas où les a_i et les b_j sont proportionnels, c'est-à-dire si soit les a_i sont tous nuls, soit il existe un coefficient  \( \lambda\)  tels que b_i = \( \lambda\) a_i pour tout i.

La démonstration la plus élégante de cette inégalité utilise le fait que le trinôme du second degré T(x) somme des termes (a_ix + b_i)² ne peut avoir deux zéros distincts (puisqu'il est toujours positif), ce qui se caractérise par le signe de son discriminant et fournit l'inégalité voulue (comme proposé en encadré).

L'inégalité de Cauchy-Schwarz permet de trouver des extrema quand des sommes de carrés sont constantes. Par exemple, déterminons les extrema de 2x + 3y + 6z si x² + y² + z² = 1. En utilisant les nombres 2, 3, 6 et x, y, z, l'inégalité s'écrit (2x + 3y + 6z)² ≤ 49, avec égalité si, et seulement si, x, y et z sont proportionnels à 2, 3, 6, c'est-à-dire s'il existe  \( \lambda\) tel que ^{\( x=2\lambda\)} ,  _{^{\( y=3\lambda\)}}  et ^{\( z=6\lambda\)} . La contrainte x² + y² + z² = 1 donne ^{\( 49\lambda^2=1\)} , soit ^{\( \lambda\)} = ± 1/7. Les extrema cherchés sont donc ± 7. On résout ainsi des questions d'optimisation tout à fait non triviales, et l'on remarque au passage que le second degré recèle encore de beaux problèmes mathématiques…