De nombreux problèmes d'optimisation proviennent de situations géométriques : minima ou maxima de longueurs, d'aires, d'angles. La plupart ont évidemment une solution algébrique, mais on peut aussi, avec un peu d'astuce, leur trouver une solution exclusivement géométrique, preuve que l'on peut optimiser sans dériver !

D'illustres exemples

Elyssa, princesse de Tyr, qui, selon la légende, fuit son frère Pygmalion après qu'il eut assassiné son époux, au IX^e siècle avant notre ère, trouve refuge dans l'actuelle Tunisie, où les autochtones ne lui concèdent que ce que pourrait couvrir… la peau d'un bœuf. Qu'à cela ne tienne, elle découpe cette peau en fines lanières pour en faire une corde de quatre kilomètres de long, qu'elle va utiliser au mieux pour encercler son territoire et y fonder la ville de Carthage, dont elle deviendra la première reine sous le nom de Didon. Le problème de Didon est l'un des plus anciens problèmes d'optimisation, dit isopérimétrique : maximiser une aire pour un périmètre donné. La forme du territoire envisagé par Didon sera un demi-cercle ayant le rivage du golfe de Tunis pour diamètre.

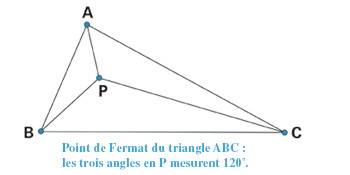Un peu plus proche de nous, cet autre magnifique problème d'optimisation a été posé pour la première fois en 1636 par Pierre de Fermat, magistrat féru de mathématiques, dans sa Méthode du maximum et du minimum : « Étant donnés trois points, en trouver un quatrième tel que la somme de ses distances aux trois points donnés soit minima. » Quatre années plus tard, Evangelista Torricelli en propose une solution géométrique, que d'autres mathématiciens après lui vont améliorer, restant souvent dans le domaine de la géométrie : Bonaventura Cavalieri en 1647, Vincenzo Viviani en 1659, Thomas Simpson en 1750, Franz Heinen en 1834… On sait donc maintenant que la solution, si aucun des angles du triangle n'excède 120°, est un unique point intérieur au triangle – appelé point de Fermat, ou encore point de Torricelli – et tel qu'on voit depuis ce point les trois côtés du triangle sous un angle de 120°.

Inattendu est cet autre problème d'optimisation, sujet du concours général 1876 de philosophie, qui comportait alors une épreuve de mathématiques. C'est le futur philosophe Henri Bergson qui en a reçu le premier prix, donnant à un problème d'extremum une solution par l'analyse, mais suggérant une autre solution, géométrique cette fois.

Il s'agissait d'évaluer les variations de forme et d'aire de la section d'un cube de côté a par un plan perpendiculaire à sa diagonale. L'élève Bergson a magistralement décrit la situation et parfaitement donné la valeur de l'aire à son maximum : la section est alors un hexagone (QRSTVL, sur sa figure) dont, dit-il, « la somme de deux côtés consécutifs est constante ». En effet, QR + RS = QR + RN = QN = BC =  _{\( a\sqrt {{2} }\)} et il en est de même pour les deux autres couples de côtés consécutifs. Le seul argument algébrique qu'il utilise alors pour déterminer l'hexagone d'aire maximale est que, à somme constante, le produit de deux nombres est maximum lorsque ces deux nombres sont égaux… ce que l'on peut aisément prouver par la géométrie (voir en encadré) ! Cet apport lui permet de conclure que la section d'aire maximale est obtenue pour l'hexagone régulier de côté  _{\( a\sqrt {{2} }/2.\)}

Deux problèmes de minimum

Voici deux nouveaux problèmes de minimum dans un même contexte (un point P à l'intérieur d'un secteur angulaire xAy donné et une droite contenant P pour former un triangle avec les côtés de l'angle). Les deux énoncés se ressemblent, à ceci près qu'il s'agit, dans le premier, de minimiser un périmètre, dans le second une aire.

Le premier problème est, à partir du secteur angulaire xAy et d'un point P qui lui est intérieur, de construire une droite passant par P, coupant [Ax) en Q et [Ay) en R, telle que le périmètre du triangle AQR soit minimum.

Imaginons une droite quelconque passant par P et coupant [Ax) en Q et [Ay) en R. Il existe un cercle (C) extérieur au triangle AQR et tangent à la fois aux droites (QR), en T, (Ax) en S et (Ay) en U : c'est le cercle exinscrit dans l'angle A du triangle AQR.

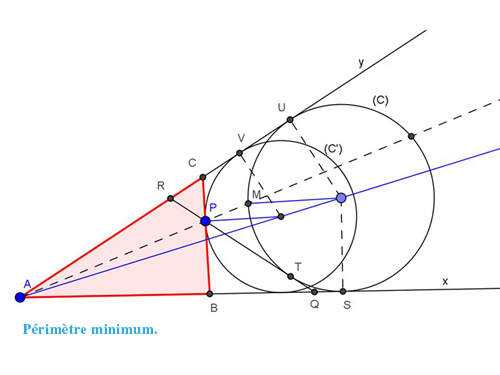
Le périmètre p de ce triangle est alors : p = AQ + QR + RA = AQ + (QT + TR) + RA = (AQ + QS) + (RU + RA) = AS + AU = 2 AU. Minimiser p, c'est donc minimiser AU.

Par ailleurs, la droite (AP) coupe (C) en deux points, dont le plus proche de A est M. En considérant l'homothétie de centre A qui transforme M en P, donc le cercle (C) en cercle (C'), et U en V, on peut affirmer que AM/AU = AP/AV, grandeur fixe k qui ne dépend pas de la position de la droite (PQ). Ainsi, AM = k AU et minimiser AU (ou le périmètre p), c'est minimiser AM.

Le minimum de AM s'obtient évidemment lorsque M est en P et le minimum de p est obtenu pour la position de la droite (PQ) tangente au cercle (C'), qui est le cercle inscrit dans l'angle xAy qui passe par P. Il se construit aisément à l'aide de son centre (tracé bleu). Le triangle solution, ABC, figure en rouge.

En partant de la même configuration (P dans l'angle xAy), il s'agit cette fois de minimiser l'aire du triangle AQR. Le minimum se produit lorsque P est milieu de la sécante [BC].

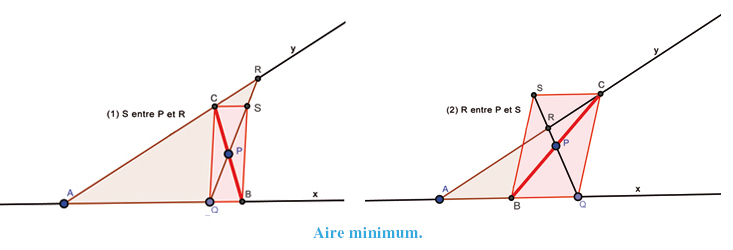
Pour démontrer que l'aire ABC correspond au minimum de l'aire AQR, on considère une sécante [QR] quelconque passant par P et on trace le parallélogramme BQCS. Deux cas se présentent selon la disposition des points A, B et Q. Soit Q est entre A et B (donc S entre P et R). Là, Aire(AQR) = Aire(AQPC) + Aire(CPR) ≥ Aire(AQPC) + Aire(CPS) = Aire(AQPC) + Aire(BPQ) = Aire(ABC). Soit B est entre A et Q (donc R entre P et S). Ici, Aire(AQR) = Aire(ABPR) + Aire(BPQ) = Aire(ABPR) + Aire(CPS) ≥ Aire(ABPR) + Aire(CPR) = Aire(ABC).

Dans les deux cas, l'aire du triangle ABC est inférieure à celle du triangle AQR.

Deux problèmes de maximum

 Cherchons maintenant l'aire maximale d'un triangle ABM inscrit dans un cercle (C). Elle est obtenue pour un triangle équilatéral CPQ inscrit dans (C). Prouvons-le en comparant les aires des triangles ABM et CPQ, où on choisit (PQ) parallèle à (AB), tous les triangles équilatéraux inscrits dans (C) ayant la même aire. Déjà, le triangle ABM a l'un au moins de ses angles de mesure inférieure à 60°. Supposons que ce soit l'angle en M. Pour comparer les aires de ABM et de CPQ, introduisons un tracé intermédiaire, celui de la parallèle menée par B à (AC), qui recoupe le cercle (C) en N. Comme AB = CN, les angles  \( \widehat{\mathrm{AOB}}\) et  \( \widehat{\mathrm{CON}}\) ont même mesure et comme \( \widehat{\mathrm{AOB}}=2\widehat{\mathrm{AMB}},\)  avec  _{\( \widehat{\mathrm{AMB}}\le60°\)} ° il vient  _{\( \widehat{\mathrm{CON}}\le120°\)} ° Or,  _{\( \widehat{\mathrm{COQ}}=120°\)} ° et donc les points C, M, N, Q, B se succèdent dans cet ordre sur (C).

On peut maintenant comparer les aires :

Aire(ABM) ≤ Aire(ABC) ≤ Aire(ACQ) ≤ Aire (CPQ) car les hauteurs relatives aux bases communes de ces triangles successifs pris deux à deux sont dans cet ordre. Ainsi, le triangle d'aire maximale inscrit dans (C) est le triangle équilatéral.

Voici pour terminer un problème un peu plus insolite : déterminer les points M intérieurs à un triangle ABC tels que le produit des distances de M aux trois côtés de ce triangle soit maximal.

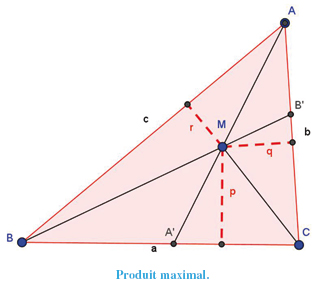Soient p, q, r les distances respectives de M aux côtés [BC], [CA], [AB] et a, b, c les longueurs respectives de ces côtés. Il s'agit de rendre maximum le produit pqr et on pourrait évidemment traiter le problème de manière algébrique. En effet, comme ar + bq + cp = 2S, S étant l'aire du triangle, on peut imaginer extraire de cette relation p en fonction de q et r et faire ainsi de la recherche du maximum de pqr un problème d'extremum d'une fonction des deux variables q et r. Mais pourquoi ne pas plutôt tirer parti des acquis géométriques précédents ? À somme égale, le produit xy est maximum lorsque x = y. Le résultat se généralise : à somme égale, le produit xyz est maximum lorsque x = y = z (voir en encadré).

Ainsi, faisant x = ar, y = bq, z = cp, 

\( (ar)(bq)(cp)\le\left(\dfrac{ar+bq+cp}{3} \right)^3\) . 

Or, ar + bq + cp = 2S, une constante. On sait donc maximiser (ar)(bq)(cp), qui est (abc)(pqr). On sait donc maximiser pqr, puisque abc est fixe. Or, ce maximum est atteint lorsque ar = bq = cp, c'est-à-dire lorsque les aires des triangles MBC, MAC et MAB sont égales. Reste à savoir pour quel point M cette égalité est réalisée.

Dans un premier temps, tout point M intérieur à un triangle peut être considéré comme le barycentre des points A, B et C affectés respectivement des coefficients égaux aux aires des triangles MBC, MAC et MAB. En effet, avec les notations de la figure, A' est barycentre de (B, A'C) et (C, A'B), donc de (B, Aire(AA'C)) et (C, Aire(AA'B)), ou encore de (B, Aire(A'CM)) et (C, Aire(A'BM)), c'est-à-dire aussi de (B, Aire(MAC)) et (C, Aire(MAB)). De même, B' est barycentre de (A, Aire(MBC)) et (C, Aire(MAB)). Le barycentre des trois sommets A, B et C, affectés respectivement des coefficients Aire(MBC), Aire(MAC), Aire(MAB), est donc à la fois sur les droites (AA') et (BB') : c'est le point M. Quand ces trois aires sont égales, le point en question est donc l'isobarycentre du triangle ABC. On conclut car le point M, intérieur à ABC, correspondant au maximum du produit de ses distances aux côtés d'un triangle ABC, est le centre de gravité de ce triangle.

Avez-vous vu des dérivées dans la résolution de ces quatre problèmes d'extremum ? Et pourtant, ils ont bien été résolus !