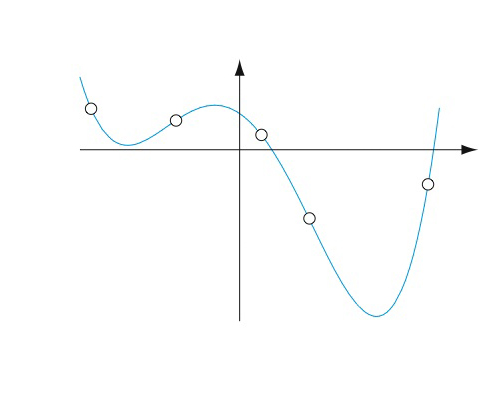
Le problème de l'interpolation polynomiale est le suivant : on connaît une fonction par ses valeurs y₀, y₁, y₂… y_N en un certain nombre N + 1 de points x₀, x₁, x₂… x_N, et on cherche un polynôme P prenant les mêmes valeurs aux mêmes points, c'est-à-dire tel que P(x_i) = y_i pour tout i compris entre 0 et N.

Par cinq points, il passe une et une seule courbe dont l'équation est un polynôme de degré au plus 4.

La condition se traduit par autant d'équations qu'il y a de points, donc N + 1. A priori, P peut être déterminé de façon unique s'il correspond au même nombre de paramètres, ce qui se produit si l'on impose à P d'être de degré au plus égal à N (le nombre de points, moins un). En effet, la question équivaut alors à un système linéaire ayant autant d'équations que d'inconnues à résoudre, ce qui, sauf cas exceptionnel, admet toujours une solution unique.

Afin d'être plus concret, considérons trois points distincts (x₀, y₀), (x₁, y₁) et (x₂, y₂), et cherchons un polynôme du second degré, sous la forme P (x) = ax² + bx + c, tel que P (x₀) = y₀, P (x₁) = y₁ et P (x₂) = y₂. La question revient à résoudre le système suivant : 

Un calcul algébrique fastidieux mais élémentaire montre que ce système de trois équations à trois inconnues a une solution unique. Une idée plus intuitive est de considérer a priori les trois polynômes du second degré L₀, L₁ et L₂ valant 1 en l'un des points et 0 en les deux autres, soit

 (valant  1 en x₀ et 0 en x₁ et x₂), et de même L₁ et L₂. Ces trois polynômes sont appelés polynômes de Lagrange. Le polynôme P suivant est alors de degré au plus 2 : P = y₀ L₀ + y₁ L₁ + y₂ L₂. Par définition, il vérifie P(x₀) = y₀, P(x₁) = y₁ et P(x₂) = y₂, comme cherché, ce qui assure l'existence du polynôme interpolateur.

Joseph-Louis Lagrange (1736–1813) a donné son nom aux polynômes interpolateurs.

Son unicité se démontre en considérant un second polynôme interpolateur Q. Le polynôme de degré au plus deux P – Q s'annule alors aux trois points x₀, x₁ et x₂, ce qui implique sa nullité (un polynôme non nul de degré 2 possède au plus deux zéros). Ainsi, P est l'unique polynôme de degré au plus 2 tel que P(x₀) = y₀, P(x₁) = y₁ et P(x₂) = y₂. Il est appelé le polynôme interpolateur de Lagrange des points (x₀, y₀), (x₁, y₁) et (x₂, y₂). De façon étonnante, Adi Shamir a utilisé cette interpolation de Lagrange en cryptographie pour partager des clefs secrètes (voir l'encadré).

L'étrange phénomène de Runge

L'approximation des fonctions est un problème légèrement différent de l'interpolation. Un segment [a, b] et une précision étant donnés, il s'agit de trouver un polynôme ne « s'éloignant pas » (sur [a, b]) de plus de de la fonction donnée. Dans ce but, on peut par exemple choisir un grand nombre de points de son graphe, d'abscisses uniformément réparties sur [a, b], et les interpoler. Malheureusement, le polynôme d'interpolation peut ne pas convenir.

Par exemple, en interpolant la fonction

sur [–1, 1] (graphe en bleu), avec cinq points d'interpolation uniformément répartis, on obtient la courbe en rouge ; avec neuf points, la courbe en vert. Plus il y a de points, plus l'approximation semble mauvaise ! Ce phénomène étrange est appelé phénomène de Runge, du nom du mathématicien qui l'a découvert.

Une façon d'y remédier est d'utiliser comme abscisses d'interpolation les zéros des polynômes de Tchebychev qui renforcent l'influence des extrémités de l'intervalle, là où se situe le phénomène de Runge. Ainsi, sur [–1, 1], il s'agit des nombres

où k varie de 0 à n – 1. Il existe aussi d'autres méthodes d'approximation qui font également appel à des polynômes. Chacune a son domaine d'application privilégié. Par exemple, les développements en série entière sont utiles pour résoudre certaines équations différentielles linéaires.

Si f est une fonction trois fois dérivable, le polynôme P_f défini par 

est appelé polynôme de Taylor de degré 3 de f. Si f est un polynôme de degré au plus 3, alors 0 est racine du polynôme P_f – f ainsi que de ses dérivées jusqu'à l'ordre trois, ce qui implique que 0 est racine quadruple de P_f – f. Comme il s'agit d'un polynôme de degré au plus 3, il est nul, donc f = P_f. Si f n'est pas polynomiale, pour obtenir une égalité, il convient d'ajouter un terme correctif à P_f, qu'on appelle le reste. Pour la fonction exponentielle, par exemple, cela donne 

et pour les fonctions sinus et cosinus, 

\( \sin x = x-\frac{x^3}{6}+S(x) \textrm{ et } \cos x = 1-\frac{x^2}{2}+T(x).\)

Un calcul de R, S et T pour de petites valeurs de x donne le tableau suivant :

Les égalités sont devenues des approximations de bonne qualité, ce qui est particulièrement frappant quand on visualise les graphes des fonctions et de leurs polynômes de Taylor. 

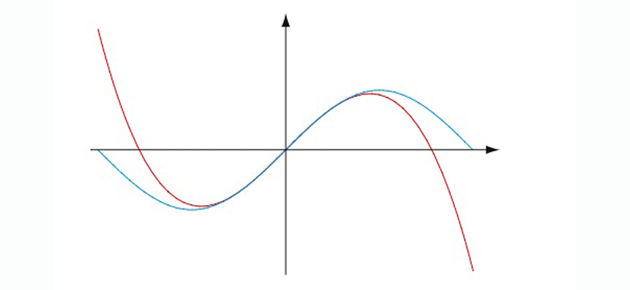
Les graphes du sinus (en bleu) et de son polynôme de Taylor de degré 3 (en rouge) se confondent au voisinage de 0.

 Le reste peut être évalué de diverses façons. Par exemple, si f a une dérivée quatrième continue, alors f = P_f + R₃ où

Cette forme du reste est attribuée à Pierre-Simon de Laplace (1749-1827). Dans le cas des fonctions exponentielle, sinus et cosinus, en reprenant les notations sans indices, cela donne :  

Il est alors facile de majorer les valeurs absolues de S et T en majorant celle du sinus et du cosinus par 1 ; les deux sont inférieures à 

Cette majoration confirme que, si x est « petit », l'approximation est excellente.

Pour l'exponentielle, la question est un peu plus délicate puisque, pour majorer l'exponentielle, il faut se restreindre à un segment, par exemple à [– a, a], l'exponentielle y est majorée par e^a, d'où l'on déduit la majoration de la valeur absolue de R par 

\( \frac{x^4}{24}e^a.\)