Les polynômes ont deux réalités, qui correspondent à deux étymologies du suffixe nôme. Selon certains linguistes, dont Albert Dauzat, les nômes des polynômes comme des monômes viennent du grec onoma, qui signifie « nom ». Cette interprétation colle à la réalité algébrique, où le X des polynômes se note généralement en majuscule et se nomme l'indéterminée ou l'inconnue. L'usage de cette lettre X remonte à René Descartes. Mais l'idée de donner un nom à l'inconnue d'un problème est plus ancienne encore, puisqu'elle viendrait de Diophante (III^e siècle), qui l'appelait arithmos, « le nombre ». Plus tard, al-Khawarizmi (IX^e siècle) la nomme shay, « la chose » en arabe. Cette pratique parvient en France grâce aux Espagnols, qui transcrivent ce mot en xay. Descartes simplifie en ne gardant que l'initiale, d'où « X ». Son usage s'étend ensuite, en particulier au monde judiciaire. En mathématiques, la lettre « X » porte le nom d'inconnue quand il s'agit de résoudre une équation, d'indéterminée s'il est question de polynômes, et de variable dans le cadre des fonctions. Un triple statut qui est parfois source de confusions !

Une autre interprétation de ces nômes vient du grec nomos, qui signifie « loi ». On peut penser alors à la fonction mathématique, donc à la « loi » de calcul. Cette interprétation colle à la réalité analytique où x devient minuscule italique et se nomme la variable.

Ces deux étymologies éclairent la différence subtile entre polynôme et fonction polynomiale. D'un côté, les polynômes sont des êtres formels, de l'autre, des lois de calcul. Ainsi, 2–3X²+4X⁴ est un objet sur lequel on peut réaliser des d'opérations (addition, multiplication, division…), mais également une fonction : celle qui, à chaque valeur substituable à X (comme 5), associe le nombre 2–3X²+4X⁴ (ici, 2-3×5²+4×5⁴=2427).
 

Des êtres purement formels

Dans le cadre algébrique, les polynômes sont des êtres purement formels. Ainsi, un monôme est une expression de la forme AXⁿ où A est son coefficient (réel par exemple) et l'entier naturel n son degré. Le degré peut être nul (comme celui de 2, car 2 = 2X⁰), égal à 1 (comme pour 5X), à 2 (dans 3X²)… Un polynôme est une somme de monômes, son degré est égal à celui de son monôme de degré le plus élevé. Dans ce cadre, les polynômes sont des êtres formels que l'on peut additionner, soustraire et multiplier facilement.

Pour calculer une somme (ou une différence), il suffit d'ajouter (retrancher) tous les monômes de chaque polynôme. Ainsi, la somme de X³ + 3X² –1 et de X² + 2X + 2 est le polynôme X³ + 4X² + 2X + 1. 

Pour calculer le produit de ces deux polynômes, c'est plus compliqué. On multiplie d'abord chaque monôme du premier par le second. Ainsi, X³ multiplié par X² + 2X + 2 donne X⁵ + 2X⁴ + 2X³. On recommence avec les autres et on regroupe le tout. On obtient X⁵ + 5X⁴ + 8X³ + 5X² – 2X – 2.

Pour la division, on opère par analogie avec la division euclidienne des entiers, celle avec reste. L'idée est d'adapter la notion de reste en disant qu'un polynôme A est « plus petit » qu'un polynôme B quand le degré de A est plus petit que celui de B. La division se pose ainsi : 

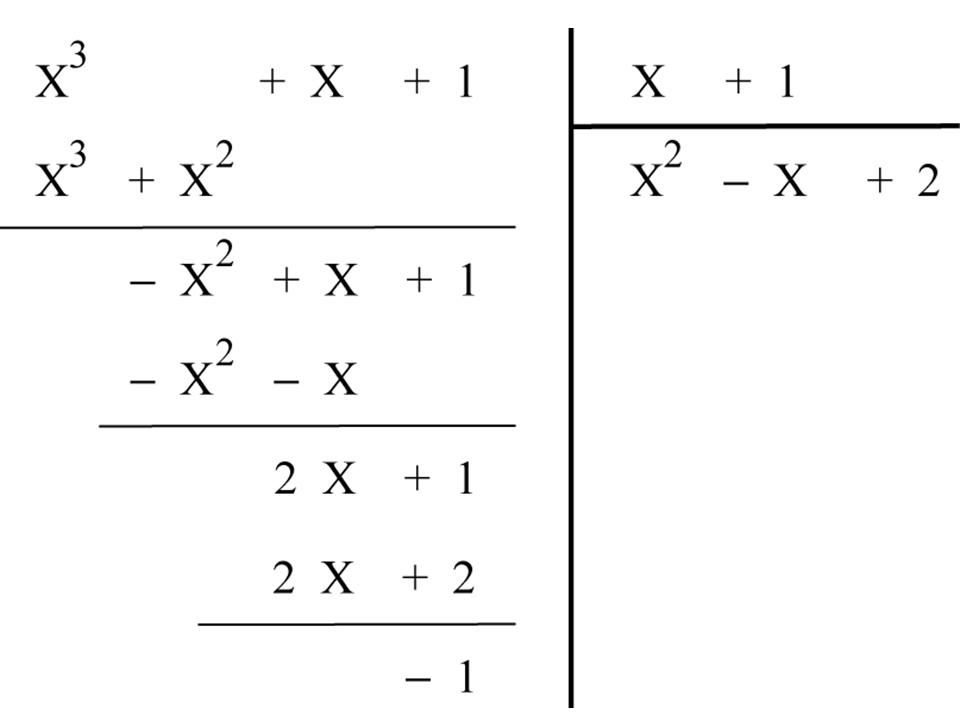
 La division euclidienne des polynômes se pose comme celle des nombres entiers : X³ divisé par X donne X², qui est donc le premier monôme du quotient. On le multiplie par le diviseur X + 1, on reporte le résultat sous le dividende avant de le retrancher à celui-ci, etc.

 Dans le cas de X³ + X + 1 divisé par X + 1, on obtient un quotient, X² – X + 2, et un reste, –1. On retrouve la relation usuelle X³ + X + 1 = (X + 1) (X² – X + 2) – 1. De façon générale, si A et B sont deux polynômes, il existe deux polynômes Q et R uniques (appelés quotient et reste) tels que A = BQ + R, où le degré de R est strictement inférieur à celui de B. Le fait que les opérations sur les polynômes ressemblent beaucoup à celles que l'on peut faire sur les entiers a conduit les mathématiciens à étudier la relation entre eux. Cette analogie a en fait un fondement bien précis : l'ensemble des polynômes et celui des entiers ont une structure commune, celle d'anneau euclidien. Il s'agit d'un ensemble muni des quatre opérations addition, soustraction, multiplication et division (avec reste). Grâce à cette structure commune avec les entiers, on peut définir les notions de multiple, de diviseur, de PGCD (plus grand commun diviseur, « plus grand » dans le sens de plus grand degré), de PPCM (plus petit commun multiple), de polynômes premiers entre eux (sans diviseurs communs) et également de polynômes irréductibles (l'analogue des nombres premiers). 

La notion de polynôme irréductible est liée à celle de zéro. Un nombre a est zéro d'un polynôme P s'il est racine de l'équation P(X) = 0, c'est-à-dire si, et seulement si, P(a) = 0. Par abus de langage, on parle aussi des racines d'un polynôme. Cela équivaut à dire que P(X) est multiple de X – a.  Le plus grand entier m ≥ 1 tel que (X – a)^m divise P (X) est appelé l'ordre de multiplicité de a. Ainsi, 1 est un zéro d'ordre de multiplicité 2 (ou zéro double) de X³ – 4X² + 5X – 2, puisque ce polynôme est le produit de (X – 1)² par X – 2. D'après le théorème de d'Alembert, un polynôme à coefficients réels ou complexes de degré n possède exactement n zéros réels ou complexes si on les compte avec leurs ordres de multiplicité. Ainsi, X³ – 4X² + 5X – 2 a trois zéros : 1 compté deux fois et 2 compté une seule fois. C'est le Français Albert Girard (1595-1632) qui conjectura ce résultat au XVIIe siècle. Le philosophe et mathématicien d'Alembert pensa le prouver au XVIII^e siècle, et lui donna son nom (en France). En réalité, sa preuve était fausse. La première démonstration correcte est l'œuvre de Gauss en 1799. 

D'après le théorème de d'Alembert, les polynômes irréductibles sont ceux du premier degré si les coefficients sont complexes. Si les coefficients sont réels, les polynômes irréductibles sont ceux du premier degré, plus ceux du second degré de discriminant strictement négatif. 

Jean le Rond D'Alembert (1717–1783, à gauche) et Carl Friedrich Gauss (1777–1855, à droite) sont les principaux artisans du fameux résultat, parfois appelée théorème de D'Alembert–Gauss, selon lequel tout polynôme de degré supérieur à 1 possède une racine complexe.

Calcul des zéros d'un polynôme

Pour les polynômes de degré 1 ou 2, il existe des formules simples donnant les zéros (voir encadré). Dans les autres cas, on utilise surtout des méthodes approchées. Pour les zéros réels d'un polynôme réel, le plus simple est de « balayer » la droite des abscisses pour détecter des changements de signe. Par exemple, X³+3X–1 est négatif en –3, positif en –2 et –1, négatif en 0 et positif en 1. Cela donne ses trois zéros, à une unité près (un entre –2 et –1, un entre 0 et 1 et un autre entre 1 et 2). On améliore la précision en coupant ces intervalles en deux et en déterminant le signe du polynôme en chaque milieu. En répétant cette opération, on trouve que le polynôme change de signe entre –2,88 et –2,87 ; il a donc un zéro égal à –2,88 à 0,01 près.

Cette méthode de dichotomie est la méthode itérative la plus élémentaire. Isaac Newton en a trouvé une plus perfectionnée. Elle consiste à remplacer le polynôme par la tangente à sa courbe représentative en un point. Par exemple, pour trouver une approximation du zéro de X³ + 3X² – 1 compris entre 1 et 2, on part du point A d'abscisse 2 du graphe du polynôme et on trace la tangente en ce point. Elle coupe l'axe horizontal en un nouveau point, ce qui fournit une approximation de la racine considérée (on trouve 1,67). Pour améliorer la précision, il suffit de reprendre le même raisonnement en partant du point B d'abscisse 1,67. On trouve 1,54.

Enfin, au XX^e siècle, le mathématicien britannique Leonard Bairstow a imaginé une méthode pour déterminer les zéros complexes des polynômes. Elle consiste à chercher des diviseurs de degré 2 puis de trouver les zéros de ces nouveaux polynômes.
 

La géométrie des polynômes

Les polynômes peuvent être vus comme des vecteurs d'un espace abstrait. On parle d'espace vectoriel pour caractériser l'ensemble de ces vecteurs (car on peut faire des additions et des multiplications par un scalaire, voir Tangente 144). Quelle est la dimension de cet espace ? On entend ici par « dimension » le nombre de paramètres nécessaires et suffisants pour définir un vecteur (par exemple, dans le plan, un vecteur est défini par deux coordonnées, donc le plan est de dimension 2). Si on ne limite pas le degré des polynômes à coefficients réels, l'ensemble qu'ils forment est un espace vectoriel de dimension infinie. Si on se limite au degré n, un polynôme est défini par ses monômes de degré 0, 1, 2, 3… n, et donc par n+1 paramètres. Ainsi, cet espace est de dimension n+1. Comme on travaille dans un espace, on peut même parler de polynômes orthogonaux : cette notion est d'une grande importance en physique où l'on rencontre les polynômes de Legendre, Tchebychev, Hermite, Laguerre et Jacobi pour résoudre divers problèmes régis par des équations différentielles. L'étude de la géométrie des espaces de polynômes permet d'apporter une compréhension nouvelle des problèmes étudiés.