Si la plupart des médias parlent de catastrophes, à Tangente on préfère évoquer les réussites ! Très récemment, le problème de l'empilement optimal des sphère identiques a été résolu par Maryna Viazovska pour les dimensions 8 et 24. Pourquoi est-ce aussi extraordinaire ? Pour le comprendre, regardons les dimensions qui nous sont familières. En dimension 2, les « sphères » sont des cercles. On sait depuis longtemps que c'est en mettant un cercle au sommet d'un réseau hexagonal que l'on obtient la plus grande compacité. Une preuve complète ne fut cependant donnée que dans les années 1940, par Lászlò Fejes Tòth (1915-2005).

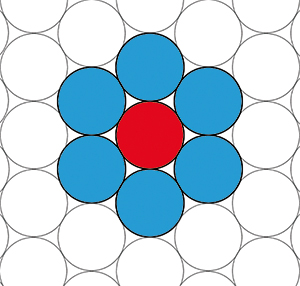La conjecture de Kepler… par Kepler

Dans Strena Seu de Niue Sexangula, publié à Francfort-sur-le-Main en 1611, Johannes Kepler conjecture que l'empilement le plus dense des sphères en dimension 3 est celui utilisé pour empiler des boulets de canon. Voici ce qu'il écrit (après traduction du latin) : « Si l'on essaie d'empiler des boulets de façon aussi dense que possible, en entassant des couches, celles-ci peuvent être constituées de boulets disposés en carrés (diagramme A) ou en triangles (diagramme B). »

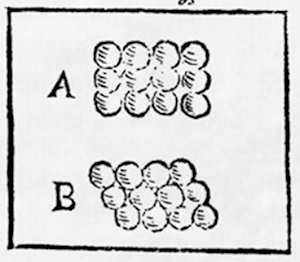« Dans le cas des carrés, un boulet serait en contact avec ses quatre voisins de sa couche carrée, un voisin de la strate du dessus et un de la strate du dessous, soit six voisins. Si l'on comprime cet arrangement, les boulets deviendront des cubes. Le réseau sera cubique et ce ne sera pas l'empilement le plus dense. Alors qu'en utilisant un motif triangulaire (diagramme B), chaque boulet est en contact avec six voisins dans sa couche et avec trois voisins dans la strate du dessous aussi bien que trois voisins dans la strate du dessous, soit douze voisins au total. Si l'on comprime cet arrangement, les boulets deviendront des dodécaèdres rhombiques [solides que Kepler a décrits dans son Mysterium Cosmographicum, publié en 1596]. »

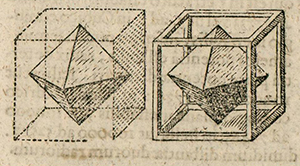
La structure est composée d'octaèdres et de pyramides. L'empilement est alors le plus dense possible : aucune autre configuration ne permettra de ranger plus de boulets dans un contenant donné. La structure globale est la suivante : les centres des sphères sont les sommets de cubes adjacents et les centres des faces, soit une structure cubique à faces centrées. Les centres des faces sont les sommets de l'octaèdre dual.
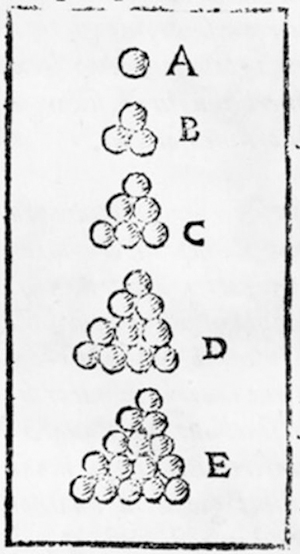
Voici comment Kepler la décrit plus précisément. Il constitue une pyramide en empilant, sur une couche de quinze boulets E, une couche de dix boulets D, puis une couche de six boulets C, une couche de trois boulets B, et enfin un dernier boulet au sommet de la pyramide. De sorte que chaque boulet est casé dans un creux constitué de trois boulets de la couche du dessous.

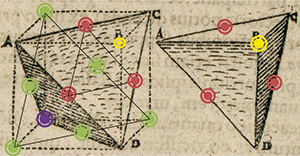
Maintenant, si l'on tourne la figure, le sommet B du cube (en jaune) peut être vu comme la couche A du Strena Seu de Niue Sexangula ; les centres des trois faces contenant le sommet B s'identifient à la couche B ; les trois sommets verts, avec les trois centres de faces restants, composent la couche C ; enfin, le dernier sommet du cube (en violet) joue le rôle du centre de la couche D. Ainsi, en partant d'un empilement de structure triangulaire, on aboutit bien à une structure cubique à faces centrées, ces deux motifs (carré et triangulaire) étant intimement mêlés.

La structure cubique à faces centrées fut découverte plus tôt par le mathématicien britannique Thomas Harriot (1560-1621). Ce dernier proposa dès 1591 un diagramme sur la façon la plus efficace d'empiler des boulets de canons. Il correspondit avec Kepler de 1606 à 1608 sur l'optique, mais a priori pas sur l'empilement des sphères.

 

8 et 24, deux cas très particuliers

Mais pourquoi est-ce aussi difficile ? Hales et son ancien étudiant Samuel Ferguson énumèrent plusieurs raisons. Tout d'abord, il est très difficile de définir rigoureusement la notion de densité d'empilement. Cela n'a été fait qu'au XX^e siècle. Ensuite, la notion de densité limite n'est pas suffisante : le fait d'enlever un nombre fini de sphères d'une région ne change pas cette densité limite. En outre, en dimension 3, il existe beaucoup d'empilements très différents qui possèdent la densité optimale. Par ailleurs, maximiser la densité est certes un problème d'optimisation, mais avec un nombre de variables infini : une infinité de sphères sont à positionner. Enfin, d'autres difficultés concernent l'existence et les propriétés d'une inégalité vérifiée par la densité locale optimale.

Si les dimensions 2 et 3 sont si redoutables, que penser des dimensions supérieures ? D'autant plus que chaque dimension semble posséder des spécificités compliquant encore le problème, comme le suggère Henry Cohn (centre de recherche de Microsoft, Cambridge, Massachusetts). Justement, Cohn et Noam Elkies (Harvard) ont réussi en 2003 à trouver des fonctions qui estiment la densité d'empilement optimale des espaces de dimensions comprises entre 4 et 36. Le problème est que les réseaux connus dans la plupart des dimensions produisent des densités d'empilement faibles, très éloignées de la densité optimale conjecturée… sauf en dimensions 8 et 24, où il existe des groupes cristallographiques particuliers : E8 pour la dimension 8 et le groupe de Leech pour la dimension 24. Dans ces cas particuliers, les densités des empilements connus sont très proches de l'optimal.

C'est là qu'entre en scène Maryna Sergiivna Viazovska. Grâce à l'utilisation des formes modulaires, dont elle est une spécialiste, et à l'analyse de Fourier, elle a trouvé une fonction donnant exactement la bonne valeur pour la dimension 8, prouvant ainsi que le réseau E₈ est le réseau optimal pour la dimension 8. La façon dont Viazovska a trouvé la fonction est qualifiée par Henry Cohn « d'une méthode d'une incroyable intelligence ». La jeune chercheuse, qui a travaillé sans relâche deux années durant sur ce problème, a publié en ligne son article pour la dimension 8 le 14 mars dernier (voir The Sphere Packing Problem In Dimension 8, sur arXiv). Elle recevait le soir même un courrier électronique d'Henry Cohn, qui lui indique que sa méthode peut être utilisée pour la dimension 24, avec le réseau de Leech. Trois semaines plus tard, ils publient avec Abhinav Kumar, Stephen Miller et Danylo Radchenko la preuve complète pour la dimension 24 (voir The Sphere Packing Problem In Dimension 24, sur arXiv). Ainsi, en plaçant des sphères de rayon √2 aux sommets du réseau E₈, c'est-à-dire aux points de coordonnées (x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈) avec tous les x_i entiers ou bien tous les x_i demi-entiers vérifiant que leur somme est un entier pair, on obtient la densité optimale de sphères en dimension 8, densité Δ égale à / 384.
Ces résultats illustrent la montée en puissance des formes modulaires dans les mathématiques contemporaines. Ces objets très abstraits mais extrêmement puissants sont aujourd'hui omniprésents en théorie des nombre.