Qu'est-ce qu'un tas de sable ? La question a l'air anodine, mais il faut pourtant bien commencer par se la poser ! Pour nos besoins, on versera délicatement du sable fin, sec, homogène sur un support découpé dans du carton rigide et calé horizontalement (la base), jusqu'à saturation. Autrement dit, on ne peut plus déposer le moindre grain de sable sur le tas formé sans que ce grain dévale la pente. La pente a alors atteint une valeur critique, la même en tout point du tas, et c'est ce qui lui vaut d'être appelée surface d'égale pente.

Un sens géométrique très sûr

Engageons-nous alors dans une séance de travaux pratiques préparatoires. Découpons dans du carton des supports variés – cercle, carré, rectangle, polygone convexe ou non, formes libres… – et observons. Le cercle produit logiquement un cône de révolution, le carré une pyramide et le rectangle une toiture où les quatre pans ont la même inclinaison. Mais, surprise, si l'on cherche à réaliser à l'identique une toiture constituée exclusivement de surfaces planes couvrant un bâtiment en forme de L, le sable s'y refuse ! Dans l'angle rentrant formé par deux pans de la toiture, le sable continue à s'accumuler jusqu'à former une surface conique (un fragment de cône de révolution) et on voit apparaître une ligne de crête curviligne, réunion de segments de droites et de deux arcs d'ellipses. 

Toiture correspondant à une base en forme de L.

Prenons maintenant une base définie par deux cercles décentrés. À nouveau, le sable fait montre d'un sens géométrique très sûr : le tas obtenu concorde parfaitement avec sa modélisation en tant que surface d'égale pente. Cette surface résulte de l'intersection de deux cônes de révolution d'axes verticaux parallèles, de même angle, leurs sommets se situant de part et d'autre du plan de base. 

Considérons un grain de sable en équilibre (instable !) en un point M sur la ligne de crête. Qu'il bascule d'un côté ou de l'autre, sa trajectoire est rectiligne et rejoint au plus près la base du tas : les deux chemins [MP] et [MQ] sont de même longueur. S'il en était autrement, le tas ne serait pas saturé : le trajet le plus long aurait une pente plus faible et le sable continuerait à s'accumuler sur ce versant.

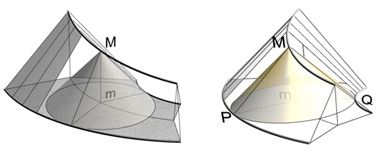
Chaque point M de la ligne de crête se projette sur la base en un point m équidistant des deux bords ; ainsi, m est le centre d'un cercle tangent aux deux bords en P et Q. M est donc le sommet d'un cône tangent à la surface le long des deux génératrices (MP) et (MQ). La surface est donc aussi l'enveloppe de la famille de cônes vérifiant cette propriété. 

Considérons une autre approche, qui s'appuie sur une propriété caractéristique de ces surfaces : leurs courbes de niveau sont parallèles. La pente étant constante, on peut gravir notre dune idéale d'un pas égal, comme quand on monte un escalier dont les marches ont une hauteur et une profondeur constantes. Les bords des marches dessinent donc des courbes parallèles. Avec notre tas qui a pour bords deux cercles, on obtient donc des courbes de niveau formées d'arcs de cercle parallèles à l'un ou à l'autre des cercles initiaux. En transformant ces courbes en gradins on obtient une nouvelle modélisation d'un tel tas de sable.

Le contour de cette « tête d'aigle » est formé d'arcs de cercle.

Quittons droites et cercles, sans complexifier outre mesure, en prenant maintenant une ellipse comme contour. L'ellipse est découpée dans le fond d'une boîte en carton, et elle est légèrement surélevée pour laisser s'écouler le sable. Une fois le tas saturé, on l'arase avec une règle en appui sur les bords du carton et on obtient ainsi une courbe de niveau parallèle à l'ellipse. 

Quant à la surface formée au centre par le sable versé sur l'ellipse, elle présente une particularité intéressante : on voit sa ligne de crête s'évanouir avant d'avoir atteint le bord. C'est un phénomène que l'on comprend assez facilement en considérant les courbes de niveau, qui sont ici des courbes parallèles tracées à l'intérieur de l'ellipse. On vérifie par la même occasion que les courbes parallèles à une ellipse… ne sont pas des ellipses ! 
 

À gauche, les parallèles à l'ellipse ressemblent progressivement à un ballon de rugby avant de se transformer en véritable ogive. L'extrémité du segment, qui est la projection de la ligne de crête, coïncide avec l'apparition d'un point anguleux. À droite, le cercle rouge correspond à la base d'un cône de révolution dont le sommet est sur la ligne de crête. Les deux segments rouges joignent le sommet aux points de contact du cercle avec l'ellipse : ce sont deux génératrices de la surface.

Si le cercle rouge se déplace vers l'extrémité du grand axe de l'ellipse, il atteint une position limite, le cercle vert, où les deux points de contact se confondent au sommet du grand axe : il s'agit du cercle de courbure de l'ellipse de rayon minimum. À vrai dire, les courbes parallèles à l'ellipse sont un peu plus sophistiquées, comme l'illustre la modélisation suivante d'une surface d'égale pente à base elliptique : les génératrices rectilignes ont été prolongées au-delà de la ligne de crête. Mais le sable, sagement, n'en garde que la partie utile.

Le vrai centre de la France

Aventurons-nous désormais vers un registre de formes très libres. Avec un peu d'expérience et de tâtonnements, il est possible d'esquisser la ligne de crête en projection sur la base, en localisant les points équidistants des deux bords (on obtient alors le squelette de la base). On voit apparaître des bifurcations de la ligne de crête, quand le cercle est tangent non pas en deux mais en trois points (voire plus). Cela correspond aux points hauts de notre crête, ses sommets. C'est avec cette approche que Robert Ferréol (qui anime le site mathcurve) a déterminé de façon indiscutable le centre de la France : c'est le centre du plus grand cercle contenu dans les frontières de l'Hexagone, et donc le sommet du tas de sable dont elles forment le contour ! Il se trouve à 10 km au nord de Bourges (Cher).