Un point se déplace, décrivant plis, replis, croisements et lignes étirées, pour composer une partie de l’espace. De cette visualisation émerge cette définition informelle d’une courbe : « morceau d’espace que l’on peut suivre de l’œil ».

Prenons à présent un grand couteau, dont on laisse la lame plus ou moins souple – plutôt un fouet ou une corde, en fait – se déployer dans l’espace. Apparaît une surface, tranche d’espace composée de tous les points ayant à un moment ou à un autre été atteints par notre corde en mouvement. Une différence avec une courbe tient à ce que la localisation d’un point de la surface requiert cette fois deux temps et non plus un seul : l’instant où le fouet passe par le point considéré, puis, une fois le fouet figé en cette position, l’instant où notre œil, glissant sur le fouet immobilisé, atteint le point visé.

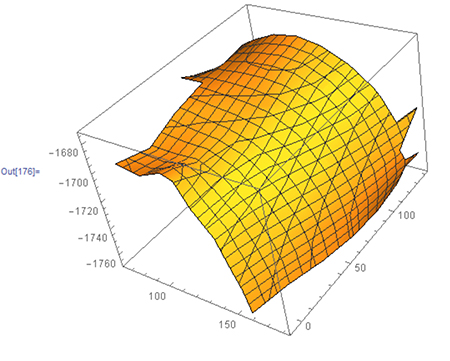
Une surface avec un système de coordonnées.

Plusieurs habits pour une surface

 Un temps pour le fouet, un autre temps pour l’œil… voilà qui en est trop pour notre perception usuelle. On définira donc plutôt les choses de façon spatiale, à l’aide d’un système de coordonnées. Il s’agit d’un « grillage » déposé sur la surface, qui permet de localiser avec deux nombres n’importe quel point de notre tranche d’espace (longitude et latitude, par exemple, pour la surface terrestre).

p.p1 {margin: 0.0px 0.0px 0.0px 0.0px; line-height: 12.5px; font: 9.0px 'Block Berthold Condensed'; color: #b88487} span.s1 {font-kerning: none}

Une même surface avec deux systèmes de coordonnées différents :

un point du carré peut être repéré selon les axes horizontaux et verticaux, ou selon les axes diagonaux.

Les spécialistes de la communication exploitent volontiers ce type d’images lorsqu’ils veulent suggérer l’idée de quelque chose de scientifique et moderne. « Quadriller » un visage humain, c’est en quelque sorte le mathématiser, donc en rendre possible l’analyse scientifique. C’est aussi ouvrir la voie aux applications telles que la biométrie. Le quadrillage peut alors se faire grillage, c’est-à-dire prison : mettre l’humain en nombres fait aisément naître la crainte qu’il s’en trouve déshumanisé.

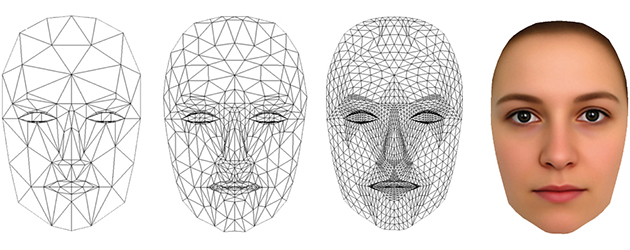L’une des graves difficultés théoriques du quadrillage d’une surface est que celui-ci n’est pas unique. Contrairement à ce qui se passe pour une courbe, où hormis les possibles variations arbitraires dans la vitesse de parcours (et le sens de celui-ci) il n’existe fondamentalement qu’une seule manière de visiter méthodiquement les points, quantité de grillages différents peuvent habiller une surface donnée.

Déterminer comment passer de l’un à l’autre est plus qu’un simple problème technique, car pour que les règles à suivre fonctionnent, celles-ci doivent capter d’une manière ou d’une autre les propriétés intimes de la surface elle-même, celles qui sont indépendantes de la manière dont elle est habillée. On parle de propriétés intrinsèques.

Cette idée de propriété intrinsèque d’une surface est à l’origine d’un résultat fondateur de la cartographie : il est impossible de constituer une carte plane d’un morceau quelconque de la surface terrestre (comme la France, par exemple). Pour démontrer cette impossibilité, on établit le caractère intrinsèque d’une grandeur appelée courbure de Gauss (voir article "Exquises surfaces minimales" par H. Lehning). On détermine alors – c’est la partie la plus facile – que la courbure de Gauss est non nulle en tout point d’une sphère, alors qu’elle est nulle en tout point d’un plan. Du caractère intrinsèque de la courbure de Gauss se déduit alors que toute représentation plane d’un morceau de sphère tel que la France altère irrémédiablement les caractéristiques géométriques du pays ainsi dessiné. Un enjeu considérable de la cartographie est alors d’adapter les cartes à leur usage, pour limiter les effets indésirables de ces altérations.

La forme de l’univers

Mère de toutes les surfaces, la sphère offre un modèle simple pour penser la question des propriétés géométriques de l’univers, en particulier celle de savoir s’il est fini ou infini. Si on pense l’univers fini, se pose le problème de décrire ce qu’il y a « au bout du monde ». Si on le pense infini, on s’expose au problème de ne jamais pouvoir le démontrer (puisque le fait de ne jamais en apercevoir les limites ne démontre pas que celles-ci n’existent pas).

Imaginons à présent un univers en forme de sphère. Ses habitants vivent dessus (ou plutôt dedans), tels des personnages de bande dessinée, légèrement courbés pour s’adapter aux contours de leur univers. Un personnage peut alors visiter cet univers sans jamais en rencontrer une quelconque extrémité, sans qu’il puisse dire pour autant que son univers est infini !

Problème réglé ? Pas vraiment : si nos personnages se meuvent bien dans un monde à la fois fini et sans bord, ce monde n’en est pas moins une sphère, elle-même située dans l’espace. Or cet espace, est-il fini ou infini ? Les personnages n’ont pas accès à cette question car ils n’ont pas accès à l’espace entier, mais balayer le paradoxe en limitant leurs possibilités de déplacement, c’est quand même un peu tricher…

Pour s’en sortir, l’étape suivante consiste à concevoir les surfaces  indépendamment d’un espace qui les contienne. En faire, donc, des objets autonomes, qui n’aient pas besoin d’un écrin extérieur pour exister.

C’est avec la notion de variété que les mathématiciens, à la suite de Bernhard Riemann au XIX^e siècle, se sont lancés dans l’exploration de ce type d’objets. Un théorème démontré par le mathématicien américain Hassler Whitney en 1936 a beau établir que toute variété peut être vue comme une partie d’un espace à quatre dimensions, cela ne signifie pas qu’il faille à toutes forces vouloir effectuer un tel « plongement » (le terme a un sens technique). La possibilité existe, mais rien n’oblige l’univers à s’y soumettre.

Aux côtés des surfaces classiques des applications courantes existent donc d’autres objets, d’un type différent. Plus abstraites, ces surfaces constituent des mondes spécifiques qui s’étudient sans qu’il y ait de sens (ou d’intérêt) à vouloir à toute force les regarder « de l’extérieur ». En somme, des mondes à deux dimensions qui ne sont pas des tranches d’espace.