
Au IV e siècle avant notre ère, Aristote pensait que le mouvement d’un objet dépendait de la nature même de cet objet. Le pendule était un problème pour lui : pourquoi la masse au bout de la ficelle, lâchée d’une certaine hauteur, ne rejoint-elle pas directement son lieu naturel, qui est le bas, mais remonte-t-elle ensuite vers le haut ?
Bien plus tard, au XVII e siècle, en observant un lustre de la cathédrale de Pise balancer alors qu’il s’ennuyait fermement à la messe, Galilée découvrit l’isochronisme des oscillations du pendule : l’ampleur du battement diminue certes au fur et à mesure du temps qui passe, mais la masse met toujours le même temps pour parcourir un aller-retour. Galilée en profita pour formuler une loi : un pendule conserve toujours la même période, laquelle ne dépend pas de l’amplitude (l’angle d’écartement du fil par rapport à la verticale).
En fait, la loi de Galilée est valable seulement lorsque l’amplitude est « faible ». À l’époque, les écarts furent constatés en mer. Pour calculer une latitude, il suffit de mesurer la hauteur du soleil tandis que, pour calculer une longitude, il faut comparer l’heure qu’il est à une heure de référence. Se posait ainsi le problème de transporter son heure de départ, d’embarquer des horloges suffisamment stables pour pouvoir conserver une heure donnée.
L’oscillation devient constante
Toujours au XVII e siècle, afin d’accomplir ses observations astronomiques, le Néerlandais Christian Huygens cherchait un instrument mesurant l’écoulement du temps avec davantage de précision. En 1656, il inventa le principe de l’horloge à pendule. Début 1659, Blaise Pascal répondit (sous un faux nom) à des questions qu’il avait lui-même posées sur la cycloïde, qu’il appelait roulette. La cycloïde est le lieu du point d’un cercle de rayon R qui roule, sans glisser, sur une droite (par exemple, la valve d’une roue de vélo).
Huygens eut alors l’idée d’essayer des gouttières cycloïdales (voir Tangente 179, 2017). Fin 1659, il fut fier d’annoncer qu’il avait obtenu des oscillations isochrones : peu importe l’amplitude, l’oscillation devient constante ! Un peu plus tard, il publia son Horologium Oscillatorium. Il y démontrait que la courbe développante d’une cycloïde est une cycloïde. En 1675, il inventa l’organe régulateur des montres, le ressort spiral, qui permet de découper le temps en intervalles réguliers du fait qu’il se tend et se détend à rythme constant.

De chaque côté du pendule, le fil épouse le dessous (les joues) des gouttières, de forme cycloïdale. Il leur est tangent en permanence et il est toujours perpendiculaire à la trajectoire car, en quelque sorte, la masse décrit un « cercle de rayon variable ». Les gouttières représentent ainsi les enveloppes des familles des droites normales à la trajectoire, c’est-à-dire les développées, le lieu des centres de courbure de la trajectoire. Or la développée d’une cycloïde est une cycloïde identique, mais translatée (d’une demi-arche à l’horizontale, et de la hauteur d’une arche à la verticale). En choisissant pour la longueur du fil quatre fois le rayon R de la cycloïde initiale, la masse du pendule décrit une nouvelle cycloïde dont le rayon est identique à celui des gouttières.
L’amplitude maximale du pendule correspond au cas où il atteint un pied de l’arche de la cycloïde. À cet instant, le fil s’appuie entièrement sur la gouttière, donc la longueur d’une demi-arche vaut la longueur L du pendule : 4R = L. La longueur de la trajectoire (de gauche à droite) vaut 8R = 2L. La période T du pendule est alors indépendante de l’amplitude. La pulsation constante est 2π / T.
Le mouvement curviligne s (t) est tel que (ds / dt)2 + ω2s 2 (t) soit une constante (ce qui définit une équation différentielle en s (t)). La somme des énergies cinétique (le mouvement) et potentielle (la gravité) est conservée. Après division par la masse, h (t) étant l’altitude et g l’intensité de la pesanteur, (ds / dt)2 / 2 + g h(t) est une constante. Finalement, ω2s 2 (t) – 2g h(t) est une constante. Pour une trajectoire « de bas en haut »,
h = 2R et s = 4R donnent
D’où
Fort heureusement, on retrouve la période d’un pendule simple pour une amplitude faible ! En effet, pour de « petites » oscillations du pendule simple, on peut confondre la courbe (le sinus) avec le segment qui relie les deux positions de la masse. Pour de plus grandes oscillations, on introduit la non-linéarité en considérant le deuxième terme du développement de la fonction sinus. On résout l’équation différentielle approchée
Cela permet d’obtenir la formule de Borda ω = ω0 (1 + θ 2 / 16 ). Par exemple, pour 90°, elle donne un facteur de 1,15. La correction est déjà bonne, mais elle est encore insuffisante à cette amplitude car le bon facteur est 1,18. En fait, au-delà de 60°, on doit utiliser les fonctions elliptiques de Jacobi. Par exemple, pour 160°, lorsqu’on se rapproche de la verticale au-dessus du point d’attache, le facteur est 2,01 : la période (l’inverse de la pulsation) est la moitié de celle d’une petite oscillation.
Une courbe étonnante…
La cycloïde est une courbe tautochrone. Tout point matériel lâché sans vitesse initiale sur la courbe arrive en un point donné (celui ayant la plus basse altitude dans le cas d’une gouttière cycloïdale) en un temps indépendant du point de départ.
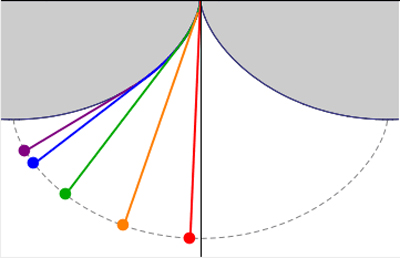
Les cinq masses mettront le même temps pour arriver en bas (trait vertical noir).
Mais ce n’est pas tout : la cycloïde est également brachistochrone. Elle représente la courbe sur laquelle doit glisser sans frottement, et sans vitesse initiale, un point matériel pesant placé dans un champ de pesanteur uniforme, de sorte que son temps de parcours soit minimal parmi toutes les courbes joignant deux points fixés. Autrement dit, bien que la ligne droite soit le plus court chemin d’un point à un autre (en termes de distance), la cycloïde est la courbe de descente la plus rapide.
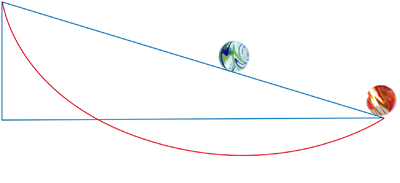
Les deux billes sont parties d’en haut au même instant.
La rouge, qui a suivi la cycloïde, vient d’arriver avant la bleue, qui suit la pente en ligne droite.