La spécificité des polyminos
Souvent, les dissections partent d'une forme géométrique qui, par un découpage habile, permet d'aboutir à d'autres formes. L'aventure des polyminos, et des pentaminos en particulier, est différente : c'est à la suite du dénombrement et de l'identification d'un ensemble de pièces que l'on va essayer de reconstituer une figure géométrique donnée.
Dès 1907, Henry Dudeney avait repéré des figures formées de cinq carrés accolés par au moins un côté (The Canterbury Puzzles, Dover, 1958). André Sainte-Laguë avait développé l'étude plus générale des polyminos dans ses cahiers d'études d'analyse combinatoire (disponibles aux archives du Conservatoire des arts et métiers), dans les années 1925. Un précurseur travaillant entièrement à la main, sans ordinateur.
Le mot polymino (ou polyomino) a été donné par Solomon Wolf Golomb (1932-2016) en 1953 à une configuration plane composée de carrés congruents juxtaposés côte à côte. Deux configurations sont comptées pour une seule si elles coïncident après rotation ou symétrie de l'une d'elles. L'ordre du polymino correspond au nombre de carrés assemblés pour former une configuration.
Les pentaminos plus forts que le Tangram !
Les polyminos peuvent être assemblés pour former de nombreuses figures, permettant une multitude de jeux et récréations. Comme on ne connaît pas de formule générale donnant le nombre de polyminos d'un ordre donné, retrouver ce nombre en tentant de dessiner de façon systématique les heptaminos (polyminos d'ordre 7, au nombre de 108), par exemple, est déjà un premier défi.
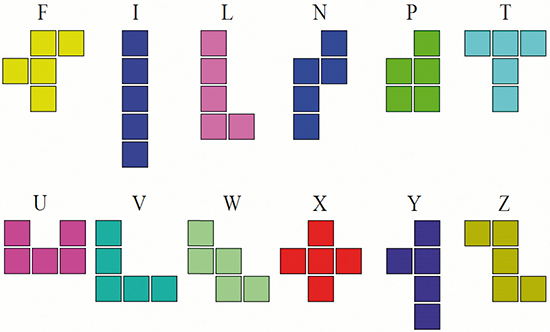
Golomb présente et théorise les pentaminos (polyminos d'ordre 5, au nombre de 12) lors d'une conférence en 1953. On lui doit en particulier le nom des douze pièces, en référence avec leur ressemblance avec des lettres de l'alphabet.
 Une mine de jeux
Une mine de jeux
Les problèmes engendrés par les pentaminos sont innombrables, les professeurs de mathématiques, y puisent à des fins didactiques, et certains logiciels peuvent y tester leurs capacités combinatoires. En voici un florilège avec des pentaminos simples (sans contraintes complémentaires de marquage individuel des carrés).
Les douze pièces forment un ensemble de soixante carreaux, qu'il est tentant d'assembler en un rectangle. Il existe 2 339 solutions pour le rectangle 6 × 10 (configuration traditionnelle de la boîte d'achat dans le commerce). Malgré ce nombre élevé, il est souvent difficile d'en trouver une ! De même, il existe 1 010 solutions pour le rectangle 5 × 12, 368 solutions pour le rectangle 4 × 15 et deux solutions seulement pour le rectangle 3 × 20.
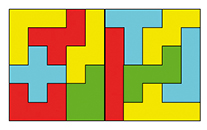
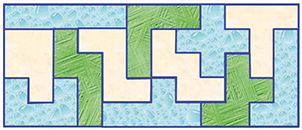
Cette solution divise le rectangle Un pavage du rectangle
6 × 10 en deux parties égales. 5 × 12.

Un pavage du rectangle 4 × 15.

L'un des deux pavages du rectangle 3 × 20.
On peut aussi s'ingénier à construire l'un des pentaminos à l'échelle 3, avec neuf pièces, en excluant la pièce tripliquée (triplication du pentamino).