Faire des choix n'est pas toujours chose aisée. On peut se tromper du tout au tout ou, au contraire, prendre des décisions qui s'avéreront optimales par la suite. L'incertitude vient du fait qu'au moment où nous nous décidons, nous ne pouvons pas savoir ce que le futur nous réserve. Sur quelles bases faire des choix, sachant que l'avenir est totalement incertain ? Les algorithmes en ligne (ou online algorithms en anglais), peu connus, sont une piste de réflexion. De manière très simplifiée, ce sont des algorithmes qui doivent accomplir des tâches, prendre des décisions, à partir d'informations qu'ils ne connaissent pas intégralement dès le début, mais qui seront dévoilées au fil de l'eau. Un point commun unit de nombreuses variantes de ce contexte : lorsque l'algorithme reçoit un « bout » des données, il doit prendre une décision irrévocable (une fois un choix fait, l'algorithme ne peut plus revenir dessus). 

Louer ou acheter un vélo ?

M. Chronos est réparateur ambulant de montres et de pendules. Son atelier se trouve dans une camionnette, avec laquelle il se déplace. Un jour, il arrive en ville et installe son outil de travail sur la place du marché, sur laquelle il peut rester le temps qu'il veut tant qu'il n'en bouge pas. Par contre, il est obligé de loger à la sortie de la ville. Chaque jour, il doit faire les trajets entre les deux lieux, assez éloignés. Il décide de se déplacer à vélo. Il a deux options : soit acheter un vélo à dix euros, soit en louer un pour un euro par jour. Le souci, c'est qu'il ne sait absolument pas combien de temps il va rester dans cette ville. Il décide que tant qu'il a des clients il reste. Si, un jour, il n'en a aucun, il partira (et n'aura alors plus besoin de vélo).

L'incertitude provient de la durée de son séjour. M. Chronos ne sait absolument pas combien de temps il va avoir besoin d'un vélo. Imaginons qu'il reste J jours. La meilleure décision à prendre, s'il connaît J à l'avance, est simple. Si J < 10, alors il est préférable de louer, ce qui coûte J euros. Si J = 10, louer ou acheter coûte dix euros. Si J ≥ 10, alors il faut acheter (dès le premier jour). Hélas, M. Chronos ne connaît J qu'à la fin du jour J, c'est-à-dire trop tard…

Voyons ce qu'il peut faire. Il décide de louer pendant dix jours, puis d'acheter le jour 11 (il n'aura donc plus besoin de louer ensuite). Cela va lui coûter, en tout, 10 + 10 = 20 euros si J ≥ 11 et J euros sinon.

En adoptant cette stratégie, M. Chronos va-t-il payer beaucoup plus que ce qu'il aurait déboursé en connaissant J à l'avance ? Notons Opt (J) le coût optimal si J était connu dès le début et C (J) ce que ça lui coûte en adoptant la stratégie précédente, sans connaître J à l'avance. Alors : Si J ≤ 10, Opt (J) = C (J) = J. De même, si J ≥ 11, Opt (J) = 10 (il faut acheter le vélo dès le premier jour) alors que C (J) = 20 (dix locations, puis achat). Ainsi, dans tous les cas, C (J) / Opt (J) ≤ 2. En adoptant cette stratégie, M. Chronos ne paiera jamais plus de deux fois ce qu'il aurait payé en connaissant l'avenir. S'il reste moins de dix jours, il paie même le prix optimal !

Réserver son canal de connexion

Fibres optiques de 576, 144 et 72 fibres empaquetées dans du nylon vert.

Le temps a passé. M. Chronos s'est reconverti et a installé des canaux de communication (de la fibre optique) entre la France et les États-Unis. Grâce à son investissement, il propose à la location m canaux, tous identiques, avec exactement les mêmes capacités. Voici l'organisation de son affaire.

Pendant la période de réservation (qui dure une semaine) ses canaux peuvent être réservés. Pendant cette période, un client peut demander la location d'un canal, n'importe lequel (ils sont équivalents), pendant une durée de p secondes. Lorsque M. Chronos reçoit une telle requête, il doit répondre immédiatement à ce client en lui indiquant quel canal il va utiliser et à partir de quelle date t il va pouvoir l'utiliser. Il construit ainsi un planning de réservation des canaux, au fur et à mesure des demandes.

Lorsque la phase de réservation est terminée, la phase d'utilisation des canaux par les clients commence : c'est la date 0 (le début). Si un client C a obtenu le canal i pour une durée p à partir de la date t, il devra être le seul utilisateur du canal i, sans interruption, entre les dates t et t + p. On parlera de connexion. Pendant la phase de réservation, il faut donc impérativement organiser le planning des (futures) connexions de manière à ce que plusieurs clients n'utilisent pas un même canal au même moment lors de la phase d'utilisation.

M. Chronos ne sait pas combien de demandes il va recevoir, ni quelles sont les durées demandées, qui peuvent être très variables d'un client à l'autre, ni dans quel ordre il va les recevoir. Il doit traiter les demandes dans l'ordre d'arrivée lors de la phase de réservation, et doit obligatoirement satisfaire chaque demande. Lorsqu'il prend une décision pour un client, celle-ci est irrévocable : il ne pourra plus, plus tard, décaler un client, le changer de canal ou annuler sa demande.

Pour rentabiliser son équipement, M. Chronos veut faire en sorte que ses canaux soient utilisés le moins longtemps possible : la date de fin de la connexion qui se termine en dernier doit être la plus petite possible. À partir de cette date, les m canaux seront à nouveau tous libres. Il pourra dès lors lancer la prochaine période de réservation.

La question est de savoir ce que doit faire M. Chronos lorsqu'il reçoit une demande de réservation avec une durée p. Sa stratégie va consister à toujours placer la réservation le plus tôt possible. Si c'est la première requête reçue, il va la placer sur le canal 1 (par exemple) à partir de la date 0, donc entre les dates 0 et p. Imaginons maintenant qu'il ait déjà placé k > 0 réservations. Dans ce cas, il va choisir le canal libre le plus tôt dans son planning, disons à la date z, et va l'attribuer à ce client, qui pourra donc l'utiliser de la date z à la date z + p. Si plusieurs canaux sont libres à une même date minimale, il en choisit un quelconque.

Comme dans le problème de location du vélo, cette organisation (gestion, prise de décisions irrévocables en suivant l'ordre d'arrivée des demandes) peut-elle le conduire à mal organiser son système ? Imaginons qu'il ait traité au total n demandes de réservation R₁, R₂… R_n dans cet ordre, chaque R_i demandant une durée d'utilisation de p_i secondes. Notons T la date de fin globale de son planning, conséquence de son système de réservation. Comparons T à la plus petite date possible de fin, notée T_min, si les n requêtes avaient toutes été connues dès le départ et s'il avait été possible de les planifier de manière optimale (en prenant tout le temps nécessaire et en les traitant dans un ordre quelconque). Bien sûr, T_min ≤ T.

Observons maintenant que T_Min est forcément plus grand que chacun des p_i : chaque demande doit être satisfaite !

Par ailleurs, les clients vont utiliser le système pendant une durée cumulée de p₁ + p₂ + … + p_n secondes en tout. Or, comme il n'y a que m canaux, nécessairement (p₁ + p₂ + … + p_n) / m ≤ T_min.

Analysons enfin le planning réalisé sur [0, T] par M. Chronos avec son algorithme. Considérons la connexion j, en rouge dans la figure, qui se termine en dernier (à la date T, donc). Soit t_j sa date de début, attribuée par l'algorithme. On a donc t_j + p_j = T. Pourquoi l'algorithme propose-t-il que la date de début de j est égale à t_j ? Son principe est de placer les réservations le plus tôt possible. Cela veut dire qu'au moment où la demande R_j a été traitée, le planning était rempli jusqu'à la date t_j, sinon elle aurait été placée avant (voir le schéma). 

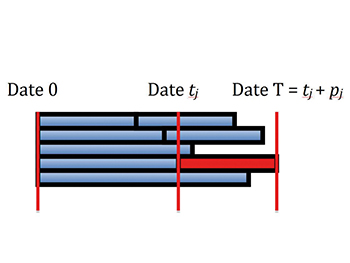
Ainsi, entre les dates 0 et t_j, les m canaux étaient déjà réservés (et ne seront plus libérés ou modifiés par la suite). Or, les m canaux ne peuvent pas être simultanément tous occupés pendant une durée supérieure à (p₁ + p₂ + … + p_n) / m secondes. Ainsi, t_j ≤ (p₁ + p₂ + … + p_n) / m.

Recollons les morceaux et mettons, dans le bon ordre, les diverses égalités et inégalités obtenues :

T = t_j + p_j ≤ (p₁ + p₂ + … + p_n) / m + p_j ≤ T_min + T_min = 2 T_min.

Cela signifie que la date T de fin produite par l'algorithme, qui est obligé de prendre des décisions à la volée en ne connaissant pas les futures demandes, est au plus deux fois celle qui aurait pu être obtenue si toutes les demandes avaient été connues à l'avance et avaient pu être traitées sans aucune contrainte sur l'ordre d'examen de ces demandes ! On le voit, ici aussi, les « dégâts » sont limités. C'est plutôt une bonne nouvelle. En fait, dans certaines situations particulières, T peut être proche de 2T_min (voir en encadré).

Ils courent, ils courent, les serveurs…

Un autre problème emblématique des algorithmes en ligne est celui des k serveurs, qui peut se décrire comme un jeu. Imaginons un plateau de jeu sur une table sur lequel évoluent k personnages, les serveurs, qui sont à des positions de départ données. À chaque étape, un point de cet espace (une demande) s'allume. Il s'agit alors de déplacer un serveur S quelconque sur ce point (S peut ensuite rester sur place). Le coût de cette opération est la distance de parcours du serveur S déplacé (le coût est de 0 si S est déjà sur place). Le coût total est la somme des coûts, donc la somme des distances de déplacement pour répondre aux demandes successives.

Les points s'allument à des endroits imprévisibles, dans un ordre quelconque. Lorsqu'une stratégie est établie, il faut comparer son coût avec ce qui aurait pu être fait au mieux si toutes les demandes avaient été connues dès le début. Vous pensez peut-être que la solution est simple : il suffit de déplacer le serveur le plus proche de la demande. Hélas, cette approche peut être très mauvaise. En effet, supposons que l'on ait deux serveurs seulement, S₁ et S₂, tous les deux initialement sur le même point A. Une première demande provient d'un point B, où S₁ est envoyé (la distance entre A et B est de dix unités). Arrivent ensuite une séquence de demandes, alternativement pour le point C puis le point B. Le point C est à distance 1 de B et à distance 10 de A. Les demandes suivantes sont donc B, C, B, C… B, C. Comme S₁ est chaque fois le serveur le plus proche, c'est lui qui est déplacé alternativement sur B et C. Le serveur S₂ ne bouge pas et reste en A car il est « trop loin ». Cela coûte en tout 10 + n, avec n le nombre de trajets entre B et C. Or, si la suite des demandes était connue à l'avance, il suffirait d'envoyer S1 sur B puis S₂ sur C, ce qui coûterait 20 au final. Les autres demandes seraient satisfaites par le serveur déjà sur place, avec un coût nul. Le coût 10 + n quant à lui tend vers l'infini. Attention donc aux idées trop simples !

Le pire rapport entre le « coût » de la solution produite par l'algorithme (qui « navigue à vue ») et le coût optimal hors ligne (offline) est appelé le rapport de compétitivité. C'est une analyse « dans le pire des cas ». Pour un problème de minimisation, l'algorithme est d'autant meilleur que ce rapport est petit.

En algorithmique, pour mesurer la capacité d'adaptation d'une méthode, on fait parfois appel à la notion abstraite d'adversaire. Le plus retors est l'adversaire adaptatif, qui va dévoiler à l'algorithme de nouvelles données en fonction de ce qu'il répond, pour essayer de le perturber le plus possible. Passer l'épreuve d'un tel adversaire (qui sait tout ce que vous faites, comment vous le faites et qui a le pouvoir de décider du futur) est un vrai défi. Les algorithmes en ligne sont étudiés depuis longtemps. Pourra-t-on en découvrir de nouveaux ? Pour répondre il faudrait… connaître l'avenir !