La théorie des ondelettes est une nouvelle approche de l'analyse des fonctions, où l'accent n'est plus mis sur les valeurs de la fonction ou de ses dérivées en un point, mais plutôt sur des moyennes sur des intervalles. Le Français Yves Meyer en est considéré comme l'un des fondateurs en 1986, ce qui lui a valu le prix Abel 2017. La théorie des ondelettes s'est extrêmement vite développée, elle a ouvert des possibilités et des applications inattendues, comme la compression de fichier, avec en particulier le format JPEG 2000.

Comment compresser un fichier

L'application la plus commune est en effet la compression de fichiers. Un fichier qui comporte beaucoup de 0 est facilement compressible : il suffit par exemple de ne pas stocker les 0, mais seulement les valeurs non nulles et leurs positions dans le fichier. Ainsi, un fichier de N nombres qui ne contiendrait que n valeurs non nulles peut n'être stocké que sur n valeurs réelles (les valeurs non nulles) et n valeurs entières (les valeurs de leur position), soit 2n valeurs. Pour compresser un fichier, on va donc chercher à créer des 0, quitte éventuellement à mettre à 0 des valeurs « proches de 0 ».

Prenons donc un fichier à compresser. Son signal sera l'ensemble des nombres contenus dans le fichier ; il représente aussi bien un son, une image, une vidéo, que toute séquence de valeurs mesurées. Les fichiers les plus simples sont à une variable, comme les fichiers sons (vingt mille valeurs par seconde pour transmettre les fréquences jusqu'à 20 kHz, limite de l'audition humaine). Si l'on ne veut transmettre qu'une seule valeur, il paraît naturel d'envoyer la moyenne m₀₀ de toutes les valeurs du fichier. Pour transmettre deux valeurs, on peut considérer la moyenne m₁₀ de la première moitié du fichier, puis celle, m₁₁, de la seconde moitié du fichier. Mais on peut aussi envoyer m₀₀ et d₁₀ = m₁₀ – m₀₀ (d₁₀ est appelé un détail). Il sera alors facile de reconstruire m₁₀ et m₁₁ (car m₁₀ + m₁₁ = 2m₀₀). Cela revient au même… sauf que, si m₁₀ = m₁₁ (non nulles), on a d₁₀ = 0. On a donc transformé une valeur non nulle (m₁₀) en une valeur nulle (d₁₀).

Quand on a une bonne idée, on ne la laisse pas en chemin, on la réutilise ! Pour transmettre quatre valeurs, on peut considérer les moyennes m₂₀, m₂₁, m₂₂, m₂₃ de chaque quart du signal, mais on peut aussi envoyer m₀₀, d₁₀, ainsi que d₂₀ = m₂₀ – m₁₀ et d₂₁ = m₂₂ – m₁₁. Et ainsi de suite, jusqu'au niveau de chaque valeur du signal.

Voici ce que cela donne concrètement pour la suite de huit nombres (10, 8, 4, 6, 4, 8, 7, 1). On a m₀₀ = (10 + 8 + 4 + 6 + 4 + 8 + 7 + 1) / 8 = 6, m₁₀ = (10 + 8 + 4 + 6) / 4 = 7, et de même m₁₁ = 5, donc d₁₀ = 1. Puis m₂₀ = (10 + 8) / 2 = 9, et de même m₂₁ = 5, m₂₂ = 6, m₂₃ = 4, d'où d₂₀ = 2 et d₂₁ = 1.

Enfin, on calcule m₃₀ = 10 / 1 = 10… jusqu'à m₃₇ = 1, puis d₃₀ = m₃₀ – m₂₀ = 1, d₃₁ = –1, d₃₂ = –2, d₃₃ = 3. Le signal « codé » est (m₀₀, d₁₀, d₂₀, d₂₁, d₃₀, d₂₁, d₂₂, d₂₃), soit (6, 1, 2, 1, 1, –1, –2, 3). Le signal originel s'en déduit.

Une petite astuce, maintenant. Dans la pratique, on organise les calculs, non pas du plus grossier au plus fin (comme ci-dessus), mais du plus fin au plus grossier, ce qui permet de ne faire que des moyennes de deux termes, faciles à réaliser à la main, particulièrement rapides à implémenter en informatique. Cela fournit l'organisation suivante. Le tableau est parcouru niveau par niveau, de haut en bas.

En noir figurent les nombres de départ, en bleu les moyennes des deux nombres situés au-dessus, en rouge et entre parenthèses les détails, qui sont aussi les demi-différences des deux nombres au-dessus.

On appelle décomposition en ondelettes (ou codage) le fait de passer des valeurs du fichier à m₀₀ et aux détails de tous niveaux, et reconstruction du signal le fait de recalculer les valeurs d'origine du signal à partir de m₀₀ et des différents détails. Ici, pour reconstruire le signal, on calcule, niveau par niveau, toutes les moyennes à partir de m₀₀ = 6 et des détails, en parcourant le tableau du bas vers le haut. On parle d'échelle ou de niveau de résolution pour le calcul des moyennes intermédiaires (échelle 0 pour la moyenne générale, échelle k pour les moyennes de 2^n–k termes et les détails correspondants). On voit poindre le vocabulaire (analyse multi-échelle, analyse multi-résolution…) cher à ceux qui utilisent les ondelettes.

Le compromis entre taille et qualité 

 Dans la « vraie vie », les fichiers sont toujours de grande taille et les détails des calculs ne sont jamais présentés. Par ailleurs, par simplicité, nos fichiers possèdent N = 2ⁿ nombres où n est un entier.

Pour compresser un fichier, c'est maintenant tout simple : après le codage, on met à 0 tous les coefficients qui sont « petits » en valeur absolue. Le fichier est stocké, transmis sous sa forme codée, et reconstruit lorsque l'on désire l'utiliser. Évidemment, le seuil en dessous duquel les coefficients sont mis à 0 dépend de l'utilisateur : plus le seuil sera élevé, plus le fichier sera compressé et plus forte sera la déformation du fichier reconstruit par rapport au fichier initial. Le rôle du « curseur » de JPEG (qualité meilleure, fichier moins compressé versus fichier davantage compressé, qualité moins bonne) est précisément de déterminer la valeur du seuil en question.

Reprenons l'exemple précédent en guise d'illustration, en mettant à 0 tous les écarts inférieurs à 1 (en valeur absolue). On obtient la séquence (6, 0, 2, 0, 0, 0, –2, 3). C'est le signal codé, compressé, stocké ou transmis. On décode alors ce nouveau signal codé, de la même façon que l'on reconstruit tout signal codé :

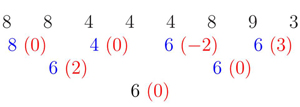La séquence qui résulte de la phase de décodage est (8, 8, 4, 4, 4, 8, 9, 3). Le signal de départ est certes déformé mais son allure générale est à peu près respectée.

 

 

Moyennes pondérées et ondelettes

Et les ondelettes dans tout cela ? Eh bien, la compression de fichiers est certainement leur application la plus spectaculaire. Examinons d'abord la démarche « analyse multi-résolution » : pour faire le codage, on a calculé des moyennes sur différentes « largeurs » du signal. À chaque largeur correspond une « échelle », ou niveau de résolution. Partant du plus large au plus fin, on va de plus en plus dans les détails du signal. Par ailleurs, pour une même échelle, on a calculé des moyennes décalées les unes par rapport aux autres. C'est exactement ce que l'on fait avec les ondelettes : au lieu de regarder les valeurs point par point d'une fonction, on va évaluer des moyennes sur des largeurs successives. De plus, pour une même largeur, on va calculer des moyennes sur des intervalles successifs (on parle d'intégrales sur des intervalles translatés). Cette approche est précisément la démarche utilisée avec les ondelettes.

Les quantités calculées plus haut sont des moyennes « standard », appelées non pondérées : on n'a pas donné de coefficient (ou poids) à chacun des termes composant la somme constitutive de la moyenne. Or, on a des résultats bien meilleurs en affectant des coefficients à certains termes (typiquement en donnant davantage d'importance aux valeurs situées près du milieu de l'intervalle où est calculée la moyenne). Les ondelettes sont précisément les fonctions qui, en quelque sorte, regroupent ces coefficients de pondération. En choisissant bien ces coefficients, on obtient des résultats encore plus performants (par exemple une meilleure compression des fichiers).

Les bases d'une théorie

Un outillage mathématique assez pointu est alors  requis pour générer de « bonnes » ondelettes (et donc trouver de « bons » coefficients). On parlera ainsi de fonctions de carré intégrable, orthogonales à leurs translatées et à leurs dilatées, denses dans L², à support borné ou à un certain nombre de moments nuls… C'est là (outre l'idée de départ !) qu'intervient Yves Meyer, qui a bâti les bases d'une théorie sur les conditions nécessaires ou suffisantes pour construire des fonctions « utiles » pour ces moyennes pondérées, et sur leur exploitation.

En fonction de l'application souhaitée (rapidité des calculs pour le codage, ou pour la reconstruction, continuité, dérivabilité des fonctions utilisées, capacité au contraire à reproduire des sauts ou discontinuités…), on définit ainsi différentes familles d'ondelettes, dont les plus connues et les plus utilisées sont sans doute les ondelettes crées en 1987 par Ingrid Daubechies.

Mais d'où vient le mot « ondelette » ? Pour des raisons liées à l'orthogonalité, ces fonctions présentent toutes des oscillations qui vont en diminuant au fur et à mesure que la distance au point central de l'intervalle augmente (voir en encadré). Un peu à la manière des vaguelettes que forme la surface de l'eau lorsque l'on jette un caillou dans un lac. Préférant le mot « onde » au mot « vague » (wave en anglais pour les vagues comme pour les ondes), le terme « ondelette » s'est imposé (wavelet dans la langue de Shakespeare). Pour les signaux examinés ici, il y a un niveau de précision ultime, celui des valeurs définissant le signal. Lorsque l'on va « coder » une fonction, on va pouvoir aller aussi loin, aussi finement que l'on veut.

Voilà pour les signaux à une variable. Mais on peut définir également des ondelettes à plusieurs variables. En effet, une image est aussi représentée par des nombres (mesurant l'intensité lumineuse) : un pour des images en noir et blanc, trois pour les images en couleur (un nombre pour l'intensité lumineuse de chaque couleur fondamentale). Au lieu de faire des moyennes de deux nombres consécutifs, il faut maintenant faire des moyennes de quatre nombres formant un carré, d'où les fameux pixels que l'on voit sur une image lorsque le seuil de mise à zéro des coefficients des détails (donc le taux de compression) entraîne des déformations visibles. Le principe général reste le même : moyenne globale de l'image suivie des différences des moyennes à des échelles successivement de plus en plus fines. Tout l'art consiste à bien choisir les différents coefficients, donc les ondelettes… La norme JPEG 2000 utilise des ondelettes (les coefficients des diverses moyennes) qui permettent à la fois une bonne efficacité compression versus déformation, et une bonne rapidité des calculs.