Les tragédies grecques savaient faire apparaître au bon moment un dieu descendu d'on ne sait où grâce à une improbable machine pour aider les protagonistes à se sortir opportunément d'une situation délicate. Quel mathématicien n'a pas rêvé de cette inspiration extraterrestre, ce deus ex machina inattendu, qui arriverait à point nommé pour lui souffler l'idée de génie qui lui permettrait de raccorder le chaînon manquant à sa démonstration ?
 

Des exemples célèbres et spectaculaires

Nous n'apprendrons pas au jeune Carl Friedrich Gauss (1777–1855) un moyen « magique » de calculer la somme des cent premiers entiers : c'est celui qu'il a, paraît-il, utilisé pour ce faire dès l'école primaire. Nous lui devons en effet ce deus ex machina historique. Pour calculer 1 + 2 + … + 99 + 100, il suffit d'additionner 1 + 100 = 101, puis 2 + 99 = 101… jusqu'à 100 + 1 = 101, pour obtenir 1 + 2 + … + 99 + 100 = 50 × 101 = 5 050. Le moyen se généralise évidemment au calcul de la somme des n premiers entiers : on additionne les nombres équidistants des extrêmes pour arriver à 1 + 2 + … + (n – 1) + n = n (n + 1) / 2. Il va sans dire, en suivant la même idée, que la somme 1 + 3 + … + (2n – 1) des n premiers entiers impairs est, elle, tout simplement égale à n² puisque la somme des termes équidistants des extrêmes est ici égale à 2n. Spectaculaire, non ?

Un résultat géométrique cette fois, et à la démonstration non moins spectaculaire, est dû au mathématicien français Gaspard Monge (1746–1818), l'un des fondateurs de l'École polytechnique. Il s'agit, étant donnés trois cercles de rayons inégaux, dont les tangentes communes extérieures se coupent deux à deux en trois points, de prouver que ces trois points sont alignés. Là, Monge a invoqué un deus ex machina faisant un détour… par l'espace. Imaginez, a-t-il dit, au lieu de trois cercles dans le plan, trois sphères de l'espace, posées sur une surface plane P. Au lieu de tangentes, parlons de cônes tangents aux sphères deux à deux, comme des cornets autour de boules de glace doubles. Les sommets de ces cônes sont donc situés sur P. En plus, il existe une autre surface plane, qui « couvre » les trois sphères en leur étant tangente : c'est le plan Π, symétrique au plan P par rapport au plan formé par les centres des trois sphères. Π contient lui aussi les sommets des trois cônes, qui seront donc alignés sur l'intersection des deux plans P et Π et, du coup, notre résultat se trouve démontré par projection !
On raisonne aujourd'hui, pour démontrer cette propriété, en termes d'homothéties échangeant deux cercles, dont les intersections des tangentes sont précisément les centres. La composition de ces homothéties montre directement l'alignement des trois centres. Il n'en demeure pas moins que l'incursion de Monge par l'espace, très imaginative, s'est avérée fructueuse en son temps.

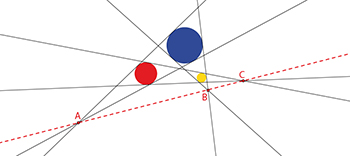
Le théorème de Monge.

Le mathématicien britannique Godfrey Hardy (1877–1947) définissait une « belle démonstration » comme étant à la fois (ô paradoxe !) « inattendue et inévitable ». Laissons à un autre mathématicien britannique, John Conway (né en 1937), le mérite de ces deux caractéristiques appliquées à la preuve qu'il donne en 1997 au théorème de Morley, « très facile à énoncer, très difficile à prouver ». L'énoncé, proposé par Morley en 1899, est effectivement simple : les trisectrices des angles intérieurs d'un triangle se coupent en trois points formant un triangle équilatéral (en rouge sur le schéma). L'idée de Conway pour le démontrer, superbe deus ex machina, a été de construire un puzzle, fait de sept triangles dont il définit les angles puis les côtés, qui devront reconstituer le triangle de départ. En bref, il part d'un triangle équilatéral, ajoute sur ses trois côtés les triangles beige (dessin de droite), imposant les angles cités sur la figure et la base égale au côté du triangle équilatéral. Il « bouche » ensuite les trous en ajoutant trois nouveaux triangles (en marron), dont il impose pour tous que les segments rouges menés du sommet (angle aigu) et faisant avec chacun des côtés des angles de 60° aient pour longueur le côté du triangle équilatéral. Des considérations géométriques simples montrent que le puzzle des sept triangles permet de reconstituer le triangle ABC. Quelle intuition !

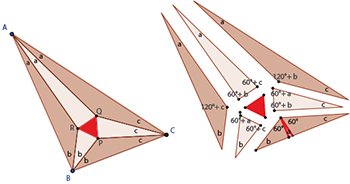
Le théorème de Morley démontré par Conway.

De toutes les couleurs

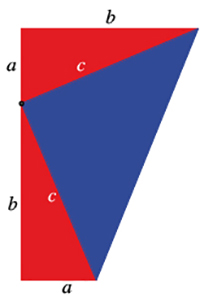
Des deux ex machina, nous en produisons tous les jours en résolvant des problèmes. Il existe en effet des arguments très souvent utilisés qui ont sur nos démonstrations l'effet mirifique d'un « haha » cher à Martin Gardner (voir Tangente 136). Nous venons d'en voir un bel exemple avec le procédé de découpage mis en œuvre par Conway. Un autre découpage, plus modeste mais néanmoins efficace, a été exhibé par… le vingtième président des États-Unis, James Abram Garfield lui-même, pour démontrer le théorème de Pythagore ! 

L'idée de James Garfield ? Mettre « bout à bout » deux triangles rectangles de côtés a, b, c et compléter la figure en un trapèze. Faites le calcul de l'aire du trapèze de deux manières différentes (calcul direct et calcul de la somme des aires des trois triangles) : vous obtenez exactement a² + b² = c². Ça fait de l'effet, non ?

Les dessins précédents comportaient beaucoup de couleurs, mais sans incidence sur la solution des problèmes. Par contre, le coloriage peut être aussi un magnifique deus ex machina. Le mathématicien allemand Arthur Engel cite quelques cas de démonstration par coloriage dans Solutions d'expert (deux tomes, Cassini, 2007 et 2010). Un sol rectangulaire, nous dit-il par exemple, est recouvert de carreaux de taille 2 × 2 et 1 × 4. On a malheureusement cassé l'un des carreaux et, comble de malchance, on ne dispose pour le remplacer que d'un carreau de l'autre sorte. Peut-on malgré cela recouvrir le sol, en réarrangeant au besoin tout le carrelage ? C'est un argument de coloriage qui va nous sauver : colorions (fictivement) le carrelage comme sur le dessin.

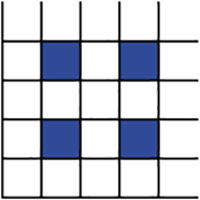
Un carreau 4 × 1 recouvre alors toujours soit aucune soit deux cases bleues et un carreau 2 × 2 toujours une et une seule case bleue. Le nombre de carreaux de chaque sorte ne peut donc être remplacé qu'en nombre pair. Dommage : on ne peut pas changer le seul carreau cassé… 

Encore une « idée magique » qui va nous tirer d'affaire : la notion d'invariant, une quantité qui ne change pas quelles que soient les manipulations du problème. Un exemple ? Les entiers de 1 à 2016 figurent sur un tableau. À chaque étape, vous en choisissez deux et les remplacez par leur différence. Au bout d'un certain nombre d'étapes, il ne reste qu'un nombre sur le tableau : pair ou impair ? Le nombre de nombres inscrits au tableau diminuant de 1 à chaque étape, c'est au bout de deux mille quinze étapes qu'il restera un seul nombre. Et là, notre deus ex machina sort du décor : la parité – c'est cela l'invariant – de la différence a – b étant la même que celle de la somme a + b, le dernier nombre qui restera aura la même parité que celle de la somme 1 + 2 + …+ 2016, qui est impaire. Le nombre restant sera donc impair. Eurêka !

Un dernier deus ex machina, très simple dans sa formulation naïve, est souvent très efficace : le principe des tiroirs ou principe des trous de pigeons. Si n + 1 pigeons sont nichés dans n trous, il existe un trou contenant au moins deux pigeons. On peut le faire intervenir dans des problèmes où on l'attend le moins : on colorie chacun des vingt-sept points du réseau ci-contre en rouge ou en noir de telle sorte qu'aucun rectangle n'ait ses quatre sommets noirs. Existe-t-il forcément un rectangle dont les quatre sommets sont rouges ?

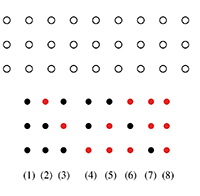
Le réseau des points et la coloration possible des colonnes.

La réponse est oui : comme il y a huit façons de colorier une colonne de trois points, et neuf colonnes, deux auront le même coloriage, et ce ne sera ni (1) ni (2) ni (3) ni (4), qui donneraient des rectangles noirs. Ce seront donc (5), (6), (7) ou (8), qui donnent tous des rectangles rouges.

On ne peut terminer cette évocation sans revenir à Martin Gardner, qui en a répertorié un grand nombre dans Haha ou l'éclair de la compréhension mathématique (Belin, 1992). En voici un exemple : dans un distributeur se trouvent six bonbons rouges, quatre blancs et un bleu, à dix centimes chacun. Combien Madame Simon devra-t-elle être prête à dépenser pour offrir à ses triplés un bonbon de chaque couleur ? L'éclair de génie qui mène directement à la solution est donné en forme de conseil par Gardner : « Rechercher la longueur du cas le plus défavorable. » C'est celui où les premiers bonbons extraits par M^me Simon sont rouge, rouge, blanc, blanc, bleu. Le sixième bonbon sera forcément rouge ou blanc, et voici les triplés de M^me Simon satisfaits, ce qui aura coûté à leur mère 60 centimes. L'imagination : voilà de quoi faire sortir du bois ce deus ex machina capable de faire céder les problèmes les plus récalcitrants.