Année 1968, un soir au YMCA de New Delhi. Trois étudiants en mathématiques, un physicien et un chimiste discutent. Un sujet anodin les conduit à parler de maths : sur les terrains de sport en ville, on joue au foot avec un ballon classique, alors que l'Europe tout entière est passée au ballon fait d'hexagones et de pentagones. En bons scientifiques, les étudiants supposent que cette structure permet de mieux approcher la forme idéale d'une sphère, mais pour en dire plus, il faudrait d'abord savoir combien d'hexagones, combien de pentagones composent l'objet. Aucun n'avait jamais pensé à examiner de près un ballon de foot… « Je vais le calculer » dit l'un des mathématiciens. « T'es pas fou ! C'est impossible ! » estime un autre. « Mais si, avec la formule d'Euler… »
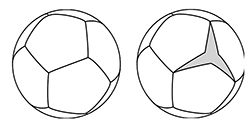
Le ballon classique dans les années 1960. Le nouveau ballon européen.
Pentagones et hexagones
« Au fond, c'est un polyèdre tracé sur la sphère. Partons de la formule d'Euler. Supposons qu'il y ait p pentagones et h hexagones. Le nombre F de faces est égal à p + h. En additionnant le nombre de sommets de toutes les faces, on trouve 5p + 6h, mais pour avoir le nombre S de sommets du polyèdre, il faut tenir compte du fait que chaque sommet appartient à trois faces, donc S = (5p + 6h) / 3. Pour le nombre total de côtés des faces, on a encore 5p + 6h, et puisque chaque arête appartient à deux faces, on divise ce nombre par 2 pour obtenir le nombre A d'arêtes : A = (5p + 6h) / 2. La formule S – A + F = 2 s'écrit donc (5p + 6h) × (1/3 – 1/2) + p + h = 2, soit p = 12. Il y a forcément douze pentagones, mais on ne sait rien du nombre d'hexagones ! »
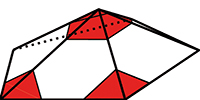
En fait, on peut avoir un nombre d'hexagones quelconque. En rognant trois faces du dodécaèdre, on dégage de la place pour un hexagone. Ce polyèdre n'est pas très beau, certaines faces y ont deux côtés consécutifs en commun. Mais la formule d'Euler n'a cure de cela : elle demande seulement que les pièces assemblées pour former un polyèdre soient simplement connexes, ce qui ici signifie que les pièces peuvent être aplaties et ne possèdent pas de trous. On peut ajouter de cette façon jusqu'à six hexagones.
En rognant les faces, on peut libérer de la place pour un hexagone.
C'est frustrant : le même genre de calcul donne sans effort la liste des cinq polyèdres réguliers. Pour notre ballon, on ne peut trouver le bon nombre d'hexagones qu'en ajoutant deux hypothèses : les pentagones ne se touchent pas, et tous les hexagones jouent le même rôle (ce qui implique que chaque hexagone touche au moins un pentagone). Avec quelques efforts, on trouve alors h = 20, puis la solution : prendre un icosaèdre régulier, à partir de chaque sommet marquer le tiers de l'arête, joindre les cinq points ainsi obtenus. Cela délimite une pyramide autour de ce sommet, qu'il suffit de retirer pour transformer les vingt faces triangulaires en vingt hexagones et faire apparaître les douze pentagones.
Ce mystérieux 2…
Quelle que soit la façon de réaliser un polyèdre, on obtient toujours, pour la quantité S – A + F, le même nombre 2. Pourquoi 2 et pas autre chose ? Déjà, plusieurs formules de décompte relatives à la sphère (au sens topologique : éventuellement déformée mais ni déchirée ni recousue) ont un 2 au second membre.
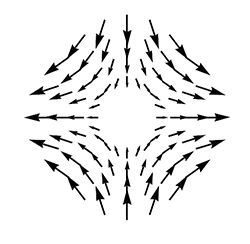
Prenons une fonction définie sur la sphère (topologique), comme la température à 0 h aujourd'hui en chaque point de la Terre. Mais la fonction que préfèrent les topologues est celle-ci : on place une sphère dans l'espace muni d'un repère, et on prend comme fonction la coordonnée z.
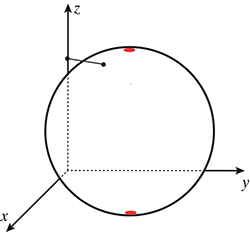
La fonction des topologues possède deux points critiques : un maximum et un minimum.
Un point critique pour une fonction, c'est un maximum ou un minimum local, pas forcément global. Pour l'altitude, le sommet d'une colline, le fond d'un lac sont de tels points. Mais il existe une troisième sorte de point critique : les cols (minimum dans une direction, maximum dans l'autre).
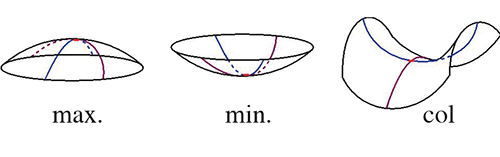
Faisons sur notre sphère une grosse bosse. Deux points critiques apparaissent pour la fonction z : un maximum local et un col. Regardez bien : impossible de faire apparaître l'un sans l'autre ! Si un bon carrossier fait disparaître la bosse, il fera en même temps disparaître le col… Même chose si la bosse est en bas (on a un minimum local et un col), ou si on ajoute d'autres bosses.
C'est un théorème : toute fonction sur la sphère possède au moins deux points critiques (un maximum et un minimum). En outre, le nombre de minima locaux, moins le nombre de cols, plus le nombre de maxima locaux, est égal à 2 !
Champs de vecteurs
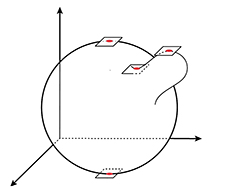
Prenons maintenant un champ de vecteurs sur une sphère. Ce n'est pas bien compliqué : on se donne en chaque point de la sphère un vecteur, c'est-à-dire une direction (tangente à la sphère) et une grandeur. On peut penser à la direction et à la force du vent sur la Terre à un instant donné. Un champ de vecteurs peut s'annuler en un point : l'œil du cyclone…
Sur le schéma, le champ de vecteurs s'annule en trois points (au moins : on ne voit pas la face cachée !). Sur la sphère en rotation ci-dessous, le champ des vitesses s'annule aux pôles Nord et Sud.
On a pour les champs de vecteurs un résultat similaire au précédent : un champ de vecteurs sur la sphère s'annule en au moins deux points. Mais il y a deux façons de s'annuler pour un champ de vecteurs :
Le champ de vecteurs s'annule. Le point d'annulation est d'indice 1, aussi bien pour les « cyclones » que pour les « anticyclones ».
Alors le nombre de points d'annulation d'indice 1 moins le nombre de points d'annulation d'indice – 1 est égal à 2.
Imaginons enfin une transformation continue de la sphère : chaque point est déplacé, mais deux points « proches » restent « proches » (pas de déchirure). Alors, si la transformation est « proche » de l'identité (chaque point n'est déplacé que d'une « petite » distance), le nombre de points fixes de la transformation est au moins 2 (pour une rotation autour de l'axe des pôles, les deux points fixes sont les pôles). De plus, les points fixes ont ici aussi un indice 1 ou – 1, et le nombre de points fixes d'indice 1 moins le nombre de points fixes d'indice – 1 est égal à 2. Cela fait beaucoup de choses égales à 2, mais cela ne nous dit pas d'où vient ce 2 !
Le champ de vecteurs s'annule.
Le point d'annulation est d'indice –1.
Les surfaces à g trous
Les notions de polyèdres, fonctions, champs de vecteurs, transformations ont un sens pour des surfaces autres que la sphère, y compris pour celles ayant un bord et celles non orientables. Mais pour simplifier laissons ces dernières de côté. Il ne reste alors comme surfaces que… la sphère, et les surfaces que l'on obtient en attachant des poignées à la sphère.
Sphères à g poignées.
Tores à g trous (autre représentation des sphères à g poignées).
La première s'appelle tore (à un trou), et les suivantes tores à g trous (g = 2, 3…). Comptons sur chaque surface le nombre de maxima, de minima, de cols de la fonction z. On trouve alors que le nombre de minima, moins le nombre de cols, plus le nombre de maxima, est égal à 0 pour le tore à un trou, à – 2 pour le tore à deux trous, à – 4 pour le tore à trois trous. En fait, tout ce qui valait 2 pour la sphère vaut maintenant 2 – 2g pour le tore à g trous. Notre mystérieux 2, c'est donc 2 – 2g pour g = 0 (la sphère possède zéro trou, ou zéro poignée). Sommes-nous satisfaits ? Pas encore !
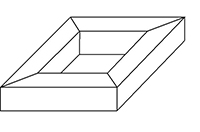
Tore à 1 trou (polyédral)
S = 16, A = 32, F = 16, S – A + F = 0
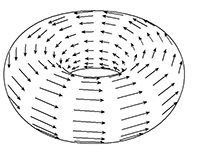
Champ de vecteurs sur le tore à 1 trou, s'annulant en 0 point.
Arrive Poincaré…
C'est Henri Poincaré qui va nous donner une réponse plus complète. « La géométrie à n dimensions a un objet réel ; personne n'en doute aujourd'hui. Les êtres de l'hyperespace […], si nous ne pouvons nous les représenter, nous pouvons les concevoir et les étudier » écrit-il en 1895 dans son article Analysis situs. À cette occasion, il crée la topologie algébrique (voir Tangente SUP 67–68). Il définit, pour les objets qui généralisent les surfaces lisses et les polyèdres en dimension n (appelés variétés et polytopes), des espaces vectoriels réels, notés H0, H1, H2… Hd (en supposant l'objet de dimension d). Un polytope possède F0 faces de dimension 0 (sommets), F1 faces de dimension 1 (arêtes), F2 faces de dimension 2 (polygones), F3 faces de dimension 3 (polyèdres)… et Fd faces de dimension d. Poincaré démontre alors la formule suivante :
S0 – S1 + S2 – S3 + … + (–1)d Sd = dim (H0) – dim (H1) + dim (H2) – dim (H3) + … + (–1)d dim (Hd).
Le second membre est appelé caractéristique d'Euler–Poincaré du polytope. Pour un polyèdre ou une surface sur laquelle on a dessiné une décomposition polyédrale, comme le ballon dégonflé, la formule devient S – A + F = dim (H0) – dim (H1) + dim (H2). Dans le premier membre, les nombres dépendent de la décomposition polyédrale choisie. Dans le second membre, ils dépendent seulement de la surface. Plus précisément : le premier espace, H0, a pour base un point (n'importe lequel, ils sont tous équivalents : on peut faire glisser le point sur la surface) ; H1 a pour base les lacets indépendants que l'on peut dessiner sur la surface (quatre au maximum pour un tore à deux trous, 2g pour un tore à g trous, là aussi, même si on est obligé d'en dessiner un pour la figure, on peut faire glisser le lacet sur la surface : c'est l'idée de faire un tour qui compte) ; H2 a pour base la surface elle-même avec son orientation. Le second membre dans la formule d'Euler (et dans les autres formules de décompte) n'est plus 2, mais « 1 + 1 » : 1 pour les points, 1 pour la dimension 2, rien pour la dimension 1. Le mystère est résolu.
D'être passé des nombres aux espaces (au XXIe siècle, on appelle ça une catégorification) permet de donner une formule des points fixes valable pour toutes les transformations de la surface, et met à notre disposition toutes les ressources de l'algèbre linéaire (voir encadré).
En théorie des nombres, on s'intéresse au nombre de points à coordonnées rationnelles des courbes algébriques, comme la courbe d'équation x5 + y5 = 1. On s'intéresse aussi au nombre de points à coordonnées dans le corps F à p éléments, où p est un nombre premier. De la même façon que l'on peut plonger le corps des réels dans celui des complexes, dans lequel toutes les équations algébriques possèdent une solution, on peut plonger F dans un corps « plus grand », F', dans lequel toutes les équations algébriques ont une solution.
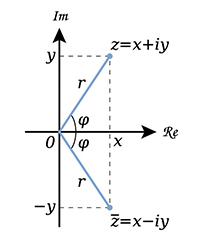
La conjugaison associe au nombre complexe x + iy le nombre complexe x – iy.
Comment reconnaît-on les nombres réels parmi les complexes ? Ce sont ceux qui sont laissés fixes par la transformation z 7 . Comment reconnaît-on les éléments de F dans F' ? Ce sont les éléments de F' qui sont laissés fixes par la transformation de Frobenius x 7 xp. En effet, pour tout élément de F, on a xp = x, c'est ce que dit le petit théorème de Fermat (voir Tangente 173). L'équation xp = x dans F' possède donc p racines distinctes. Comme F' est un corps, elle ne peut pas en avoir d'autres !
L'idée fantastique de Weil
André Weil en a tiré cette idée fantastique. Définissons C la « courbe » (ou ensemble) formée des couples (x, y) tels que x et y soient dans F et que x5 + y5 = 1. Définissons de même C' (en remplaçant F par F'). Les points de C sont les points fixes de (x, y) 7 (xp, yp) appliquée à C'. Et si la formule des points fixes de Lefschetz s'appliquait ? Le nombre de points fixes de T serait alors égal à tr (T0) – tr (T1) + tr (T2) pour des transformations linéaires T0, T1 et T2 adéquates.
Il faut d'abord disposer des trois espaces H0, H1 et H2. Qu'à cela ne tienne ! Prenons l'ensemble S des points (x, y) à coordonnées complexes tels que x5 + y5 = 1. Qu'est-ce que les nombres complexes ont à voir là-dedans ? On n'en sait rien, mais ça marche ! S est une surface (de même que l'ensemble des complexes est un plan) et c'est même un tore à deux trous (privé de quelques points, mais laissons), et dim (H0) = 1, dim (H1) = 4, dim (H2) = 1.
Comment définir maintenant T0, T1 et T2 ? C'est là que ça se corse. C'est d'ailleurs la nécessité de définir d'une façon purement algébrique (en oubliant la topologie des surfaces) les éléments se trouvant au second membre de la formule des points fixes suggérée par Weil qui a conduit Alexander Grothendieck à entreprendre son immense travail de refondation de la géométrie algébrique (voir Tangente 162), travail que l'on peut considérer comme réalisant la fusion de la topologie et de l'algèbre…