
Depuis les années 1980, la France participe aux enquêtes TIMSS et PISA sur l'enseignement des mathématiques. À cette occasion, des palmarès sont publiés. Pendant quelques jours, ils font les délices des médias, bousculent et inquiètent les responsables des systèmes éducatifs, mais, très souvent, ils laissent les enseignants et les parents interloqués, sinon dubitatifs. Tous se demandent si leur pays est vraiment aussi performant (ou aussi peu performant) que le disent ces enquêtes. L'œil fixé sur le thermomètre, ils se demandent si la hausse ou la baisse observée entre deux enquêtes est, ou non, significative, et significative de quoi…
Ce que mesure le thermomètre
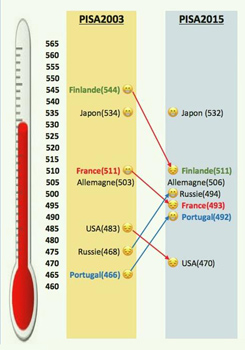 Sur l'échelle de « littératie mathématique » de PISA (le thermomètre), entre 2003 et 2015, la France est passée de l'indice 511 à l'indice 493, tandis que la Russie est passée de 468 à 494. L'analyse des statistiques montre que ces différences sont significatives : quelque chose a vraiment bougé dans les résultats de l'enseignement des mathématiques dans ces pays. Mais quoi exactement, et pourquoi ? Enfin, quels enseignements est-il possible de tirer de ces résultats pour l'action ?
Sur l'échelle de « littératie mathématique » de PISA (le thermomètre), entre 2003 et 2015, la France est passée de l'indice 511 à l'indice 493, tandis que la Russie est passée de 468 à 494. L'analyse des statistiques montre que ces différences sont significatives : quelque chose a vraiment bougé dans les résultats de l'enseignement des mathématiques dans ces pays. Mais quoi exactement, et pourquoi ? Enfin, quels enseignements est-il possible de tirer de ces résultats pour l'action ?
Heureusement, les enquêtes PISA et TIMSS ne se contentent pas de livrer des palmarès et des échelles, elles produisent aussi des informations sur le fonctionnement des systèmes éducatifs et sur les relations observées entre ces informations et les acquis observés chez les élèves. Ainsi, elles mettent en évidence la relation (statistique) qui existe entre les acquis et la taille des classes, ou l'effort fait par le pays pour la formation des enseignants, ou encore le plaisir que prennent les élèves à aller à l'école ou à faire des mathématiques. Ces variables, dites contextuelles, sont nombreuses (les rapports complets des enquêtes se mesurent en milliers de pages, qu'il convient d'éviter de lire trop rapidement).
Les origines, les promoteurs de ces enquêtes, comme leurs objectifs et les conceptions éducatives qui président à leurs réalisations, sont précisés dans les encadrés ci-contre. Mais surtout, regardons quelques questions utilisées pour évaluer les compétences et les connaissances des élèves.
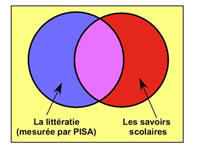 Dans le cas de TIMSS, l'évaluation des élèves porte sur leurs connaissances et leurs savoir-faire dans le domaine mathématique, et cela par rapport à des contenus d'enseignements plus ou moins communs parmi les pays concernés. Les enquêtes prennent en compte les différences curriculaires (programmes d'enseignements et autres caractéristiques liées aux systèmes éducatifs).
Dans le cas de TIMSS, l'évaluation des élèves porte sur leurs connaissances et leurs savoir-faire dans le domaine mathématique, et cela par rapport à des contenus d'enseignements plus ou moins communs parmi les pays concernés. Les enquêtes prennent en compte les différences curriculaires (programmes d'enseignements et autres caractéristiques liées aux systèmes éducatifs).
PISA, de son côté, évalue la littératie, à savoir l'« aptitude à comprendre et à utiliser l'information écrite dans la vie courante, à la maison, au travail et dans la collectivité en vue d'atteindre des buts personnels et d'étendre ses connaissances et ses capacités ». Il ne s'agit donc pas de connaissances ni de compétences purement scolaires. PISA évalue une partie seulement des acquis mathématiques, mais une partie essentielle sans laquelle il est difficile de construire autre chose.
Des exemples très concrets
L'intérêt principal des enquêtes internationales réside dans le fait qu'elles sont… internationales ! Au-delà des critiques et des mises en cause, parfois justifiées, elles obligent à un certain décentrement : voir ailleurs ce qui se fait et comment ça marche, pour mieux comprendre ce qui se passe chez nous et comment améliorer la situation. Elles complètent et éclairent les études nationales, comme celles menées par la Direction de l'évaluation, de la prospective et de la performance (ministère de l'Éducation nationale).
Voyons une question de TIMSS posée au CM1 en 2015 (question M061167, © IEA) : « Yassine commence à écrire une suite logique de nombres : 6, 13, 20, 27… Il ajoute à chaque fois le même nombre pour obtenir le nombre suivant. Quel est le nombre suivant qu'il devrait écrire dans sa suite logique ? »
Ce type de question n'est pas fréquent en France, sinon dans les exercices ludiques des magazines. Il est par contre beaucoup plus fréquent dans les pays bien classés.
Voici quelques-uns des taux de réussite enregistrés (non, les élèves européens ne sont pas plus stupides que les élèves coréens du même âge ! Ces résultats renseignent surtout sur la précocité ou le retard apporté à certains apprentissages selon les pays) :
| Allemagne 2% |
France 15% |
Russie 33% |
Singapour 64% |
Corée 67% |
La France n'a pas participé à l'enquête TIMSS de quatrième en 2015. Voici toutefois une question typique de ce niveau (question M062074, © IEA) : « Jeanne a décrit la représentation graphique d'une fonction : la représentation graphique est une ligne droite ; la représentation graphique coupe l'axe des y au point d'ordonnée 3. Quelle peut être la fonction étudiée par Jeanne ? A. y = x2 + 3 ; B. y = 3x + 1 ; C. y = 3x2 – 1 ; D. y = x + 3. »
La question confond « fonction » et « équation de courbe représentative d'une fonction » ; cela est habituel dans nombre de pays. Il est souvent difficile de traduire les questions de façon correcte d'une langue à une autre tout en conservant l'équivalence recherchée en matière de complexité…
Les taux de réussite montrent que ce type de question est assez habituel dans de nombreux pays dès la classe de quatrième (alors qu'il ne serait pas acceptable en France) :
|
Italie |
Irlande 51% |
Singapour 58% |
Russie 60% |
Japon 66% |
Voici enfin une question de TIMSS advanced 2015 (terminale S, question MA33121, © IEA) :
« Soit a une constante non nulle. Déterminer les abscisses des deux points d'intersection des courbes d'équation y = 106ax et y = x2/106. »
Il y a deux solutions, x = 0 et x = 1012a. La présence d'un paramètre, a, qui ne joue aucun rôle a pu gêner les élèves français :
|
France |
Portugal 13% |
Russie |
Pour TIMSS advanced, les taux de réussite sont délicats à interpréter : le pourcentage de jeunes d'une classe d'âge qui suivent un enseignement scientifique en fin d'études secondaires est très variable d'un pays à l'autre.
QCM versus rédaction
Pour PISA comme pour TIMSS, les élèves ont environ soixante questions à traiter en deux heures (soit en moyenne deux minutes par question). Pour moitié, ou moins, ce sont des questions à choix multiples (QCM) et, pour le reste, des questions ouvertes à réponse courte souvent réduite à un mot ou un nombre (une ou deux phrases dans les cas extrêmes). Les élèves français sont davantage entraînés à la rédaction et à la démonstration, dimensions qui sont… totalement absentes tant de PISA que de TIMSS !
TIMSS s'ancre pleinement dans les mathématiques. A contrario, pour PISA, les mathématiques ne sont qu'un outil susceptible de contribuer à la résolution de problèmes que l'élève est susceptible de rencontrer dans sa vie. Le contexte comporte des éléments utiles pour la résolution, et des éléments inutiles. L'encadré ci-contre (Le cargo à voile) présente trois questions, dépendant d'un même contexte.
Voici quelques taux de réussite observés :
| France | Allemagne | Canada | Finlande | Japon | |
| Question 1 | 54% | 64% | 58% | 73% | 57% |
| Question 2 | 45% | 54% | 57% | 50% | 53% |
| Question 3 | 13% | 20% | 21% | 16% | 19% |
La question 3 aurait fait un bon problème de certificat d'études dans les années 1960, avec cependant de nombreuses donnés inutiles. Les taux de réussite montrent bien qu'elle est d'ailleurs loin d'être facile pour des élèves de 15–16 ans…
Les résultats d'ensemble de ces trois enquêtes sont très inquiétants, tant en ce qui concerne la faiblesse des résultats qu'en ce qui concerne la distance, inégalée dans le monde, entre les plus forts et les plus faibles de nos élèves.