La théorie de l'information est née d'un article en deux parties que Shannon a publié en 1948, quand il était chercheur aux Laboratoires Bell. Il a montré comment la notion jusqu'alors vague d'information pouvait être définie et quantifiée avec précision. Il a établi l'unité essentielle de tous les moyens et canaux d'information : les textes, les communications téléphoniques, les messages radio, les photos, les films… peuvent être codés dans le langage universel des chiffres binaires, ou bits, terme qu'il est le premier à utiliser. Il a mis en avant l'idée que, une fois que l'information était devenue numérique (transformée en une suite de bits), elle pouvait être transmise (ou stockée) avec un taux d'erreur qui pouvait être rendu arbitrairement petit, et ce même si le canal (ou le moyen de stockage) lui-même est imparfait, source de bruit et d'erreur. Ce saut conceptuel a conduit directement à des moyens de communication et de stockage robustes et rapides.

Trop de bruit !

La théorie de l'information de Shannon a montré que les limites ultimes de capacité de communication (et de stockage) de l'information étaient liées au bruit présent dans les canaux. Au début des années 2000, la recherche sur la théorie de l'information a frôlé la mort : il a semblé que l'on avait atteint ces limites de capacité. Cependant, des développements récents prouvent que le bruit peut s'avérer bien surprenant, voire même… utile ! En effet, si le bruit considéré par Shannon était essentiellement blanc, c'est-à-dire ne possédait aucune structure, le bruit que l'on observe dans nombre d'applications peut être plus complexe et structuré, et être capable de porter en lui-même une certaine forme d'information à travers ses corrélations. La recherche est repartie, dans les domaines de la communication, de l'imagerie et de la séismologie notamment.

^{A mathematical theory of communication.
Claude Shannon, Bell Systems Technical Publications 27, 1948.}

Né en 1916, Claude Elwood Shannon est un enfant éclairé, curieux. Il bricole un télégraphe avec du fil de fer barbelé pour communiquer avec son ami qui vivait à un kilomètre. Entré à l'université du Michigan en 1932, il obtient deux licences, en mathématiques et en ingénierie électrique. Il part faire son master au Massachusetts Institute of Technology (MIT) à Boston en 1936. Il effectue un stage chez Vannevar Bush, concepteur d'un ordinateur analogique, appelé analyseur différentiel. C'est une grosse machine d'une centaine de tonnes conçue pour produire des courbes qui sont des solutions approchées d'équations différentielles du second ordre, que l'on retrouve souvent en physique. Son travail consiste à activer les commandes, des interrupteurs qui activent eux-mêmes des relais (des interrupteurs commandés électriquement), pour mettre en œuvre la résolution d'une équation particulière. À l'issue de son stage va naître en 1937, selon les termes du professeur Howard Gardner de Harvard, le mémoire de master le plus important du XX^e siècle, intitulé Une analyse symbolique des circuits à relais et de commutation.

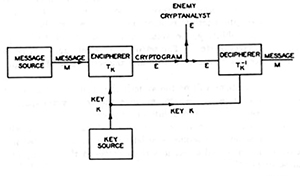
En 1939, Shannon confie à Vannevar Bush qu'à ses moments perdus il travaille sur l'analyse des systèmes généraux de transmission de la connaissance. Dans sa lettre, il décrit la forme générale des systèmes de communication, et souligne les difficultés essentielles liées au fait que les systèmes réels sont toujours affectés par des distorsions et du bruit.

Au début de la Seconde Guerre mondiale, il est affecté à un projet d'étude sur les mécanismes de contrôle de tir de canons antiaériens. Il s'agit de mettre au point une machine prenant en entrée des données issues de télémètres ou de radar et permettant de lancer les obus sur une trajectoire interceptant la cible en mouvement. Shannon y voit un « cas particulier de transmission, de manipulation, et d'utilisation de l'information ». Il rencontre en 1943 Alan Turing, en visite aux États-Unis après avoir cassé pour les Britanniques le code Enigma utilisé par les Allemands. Shannon note qu'un « système secret est presque identique à un système de communication avec bruit ».

En parallèle de ses travaux en contrôle de tir et en cryptanalyse, il construit progressivement sa théorie générale sur les communications. Dans son rapport final, A mathematical theory of cryptography, classé secret défense en 1945, il annonce son intention de « développer ces résultats dans un prochain mémoire sur la transmission de l'information ».

^{Le rapport classifié de 1945.} 

  ^{L'article publié en 1948. La première figure ressemble étrangement à la celle du rapport classifié de 1945…}

1948 : les fondements

La théorie de l'information est née d'un article en deux parties que Shannon a publié en 1948, quand il était chercheur aux laboratoires Bell. Ces derniers sont le département de recherche et développement de la compagnie de téléphone américaine de l'époque AT&T, fondée par Alexander Graham Bell en 1885, qui avait le monopole des services téléphoniques en Amérique du Nord. 1948 est aussi l'année de la découverte, par ces mêmes laboratoires Bell, du transistor, composant électronique de base, beaucoup plus pratique et compact que les tubes à vide qui existaient alors, et qui a permis le développement des circuits intégrés. Ils sont donc à la pointe de la recherche dans tous les domaines des communications.

On ne voit pas tout de suite le rapport entre la télévision, où le but est de transmettre un signal vidéo par ondes hertziennes, et le téléphone, où le but est de transmettre un signal sonore sous la forme d'une modulation d'un courant électrique passant dans un câble en cuivre. L'article de Shannon montre que ces problèmes peuvent être abordés de manière universelle et qu'il existe une solution optimale : le passage au numérique. Il faudra néanmoins attendre une cinquantaine d'années pour que la puissance des résultats mathématiques de Shannon puisse s'exprimer pleinement !

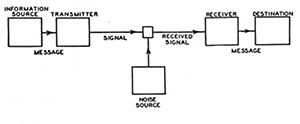
Prenons une information : un son, une image, une vidéo, un texte. Comment la transmettre sur une grande distance sans la détériorer ? On utilise généralement un processus physique très efficace : les ondes électromagnétiques. Dans le cas de la radio, un journaliste parle à ses auditeurs. Pour transmettre ce message vocal, il utilise un microphone, qui transforme sa voix en un signal électrique, envoyé à une antenne qui émet un signal électromagnétique (une onde radio). Ce signal voyage à la vitesse de la lumière, est reçu par des postes de radio, qui le transforment en un signal électrique, qui est envoyé à un haut-parleur, qui le transforme en un message vocal audible pour l'auditeur. Tous les systèmes de transmission de l'information fonctionnent sur ce principe ! C'est ce que résume le schéma de l'article de Shannon de 1948.

Il existe une multitude de types d'informations, mais aussi une multitude de canaux de transmission : des câbles électriques (pour le téléphone fixe), des fibres optiques (pour Internet), des microondes (pour les téléphone portables), des ondes hertziennes (pour la télévision), des ondes radioélectriques (pour la radio). Et une multitude de moyens de transcrire une information en un signal ! Quel est le meilleur moyen ? Pour répondre à cette question, il faut d'abord la poser précisément, et définir ce qu'est une information.
 

Passer au numérique ! 

Le problème est celui de la communication entre une source et un récepteur : la source émet un message que le récepteur lit. On voudrait quantifier l'« information » que contient chaque message émis. Le cas le plus simple est celui où le récepteur attend une information de type oui/non, chacune étant a priori aussi vraisemblable que l'autre. Lorsque la source transmet soit un oui soit un non, on considère que le récepteur reçoit une unité d'information (un bit) : on a a priori un ensemble de deux possibilités, et l'une d'elles se réalise. La quantité d'information selon Shannon est le nombre de bits nécessaire et suffisant pour représenter un message.

C'est devenu une évidence aujourd'hui : on mesure les vitesses de transmission de données en bits par seconde, quel que soit le message : voix, musique, film, texte. On mesure la capacité de stockage d'un disque dur ou d'une mémoire flash en octets (un octet vaut huit bits), quel que soit le type de données. La théorie de l'information de Shannon montre que toute information, tout message, peut se laisser décomposer en une suite d'informations binaires, et que c'est la manière optimale pour représenter, comprimer et transmettre de l'information. Le message de l'article de Shannon est donc : il faut passer au numérique !

Une fois que l'information est devenue numérique, elle peut être transmise ou stockée avec un taux d'erreur qui peut être rendu arbitrairement petit, et ce même si le canal ou le moyen de stockage est imparfait, source de bruit et d'erreur. Ce saut conceptuel a conduit directement à des moyens de communication et de stockage robustes et rapides. S'il n'y a pas de bruit ou d'erreur, on peut transmettre et stocker tout message contenant une quantité d'information H (au sens de l'entropie de Shannon) sous la forme de  \( \lceil H \rceil\) bits (où \( \lceil H \rceil\) est l'entier immédiatement supérieur à H). La théorie de l'information de Shannon montre que les limites ultimes de capacité de communication (et de stockage) de l'information sont en fait liées au bruit présent dans les canaux de transmission (et dans les erreurs commises pendant les procédures d'écriture et de lecture pour le stockage). Le bruit est inévitable, quel que soit le medium ou le canal de transmission : des ondes hertziennes utilisées pour la télévision (analogique ou TNT) aux ondes électromagnétiques par la radio, des microondes pour la téléphonie mobile à l'antenne râteau sur votre toit, votre poste de radio comme l'antenne de votre téléphone mobile reçoivent un signal auquel se superpose du bruit. Créé par tout un tas de sources parasites, il était sensible (visible ou audible) du temps des communications analogiques : on entendait un grésillement au téléphone, on voyait de la neige sur le poste de télévision. Vous n'êtes pas le seul utilisateur ! L'analogie avec l'effet cocktail est saisissante : vous essayez de parler avec une personne lors d'une soirée, c'est bondé, votre conversation est brouillée par celle des autres convives…
 

Dans la téléphonie 4G

La compréhension mathématique de la notion d'information et la modélisation mathématique du bruit ont permis à Shannon de définir une frontière entre ce qui est possible et ce qui est impossible de faire en termes de capacité de transmission ou de stockage de l'information. Il en a donné les capacités ultimes en fonction du niveau de bruit, à travers des théorèmes toujours d'actualité. C'est seulement dans les années 1990 que des algorithmes appelés turbo-codes (inventés par Claude Berrou et Alain Glavieux) ont permis d'approcher la capacité théorique de Shannon. Ils sont utilisés dans la téléphonie mobile 3G/4G.